Pomocy!!
MONIA: Wykaż, że promień okręgu w pisanego w trójkat prostokatny o przeciwprostokątnej c i
przyprostokątnych a i b wyraża się wzorem r=a+b−c/2
7 mar 21:26
Edek: | | c | | a+b−c | |
r=a+b− |
| czy r= |
| ? |
| | 2 | | 2 | |
7 mar 21:38
MONIA: to drugie
7 mar 21:40
Edek:
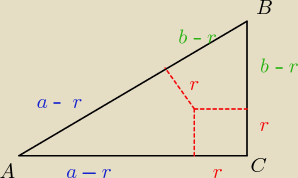
|AC|=a
|BC|=b
|AB|=c
c=a−r+b−r
c=a+b−2r
2r=a+b−c
7 mar 21:47
Basia:
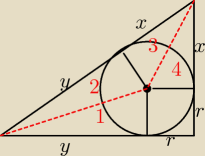
2x+2y+2r = a+b+c
2(x+y)+2r=a+b+c
2c+2r=a+b+c
2r=a+b−c
a wynika to z tego, że tr.1 i tr.2 są przystające
oraz tr.3 i tr.4 są przystające
7 mar 21:56
MONIA: Dziękuje P. Edkowi.
Nie wpadłam na to, mam jeszcze jedno zadanie.
Długości boków pewnego czworokąta są kolejnymi liczbami naturalnymi. Czy w ten czworokąt można
zapisać okrąg?
7 mar 22:00
MONIA: Dziękuje również Pani Basi
7 mar 22:01
Edek:
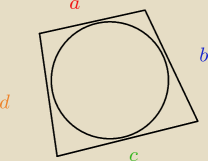
chodzi Ci o to czy w taki czworokąt można wpisać okrąg
warunkiem takiego stanu rzeczy jest aby przeciwległe boki takiego czworokata były sobie równe
czyli a+c=b+d
zakładamy u nas
a=a
b=a+1
c=a+2
d=a+3
otrzymujemy
a=a+2
a+1=a+3
niestety taki układ nie będzie miał rozwiązania w N, czyli takie czworokąt nie istnieje
7 mar 22:07
Basia: Edek, tam jest błąd:
a≠c i b≠d tylko
a+c=b+d
a+a+2=a+1+a+3
2a+2=2a+4
2=4
sprzeczność
albo jeszcze prościej
n+(n+2)=(n+1)+(n+3)
2n+2=2n+4
2=4
sprzeczność
7 mar 22:18
Jack: raczej tak powinno wyglądać, że nieprawda, że a+a+2 = a+1 +a +3.
7 mar 22:20
MONIA: Dziękuje i proszę jeszcze o rozwiązanie tego beznadziejnego zadania Na pewnym trapezie można
opisać okrąg i w ten trapez można wpisać okrąg Podstawy maja 7 i 3 oblicz długości ramion.
7 mar 22:26
Jack: Musi być to trapez równoramienny... Skorzystaj z równości podanej przez Edka a+c=b+d.
7 mar 22:32
Basia:
a=7
b=3
jeżeli trapez jest wpisany w okrąg to jest równoramienny ⇒ c=d
jeżeli jest opisany na okręgu ta a+b=c+d
stąd
2c=10
c=5
7 mar 22:36
MONIA: skad my wiemy ze to jest trapez rownoramienny
7 mar 22:37
MONIA: ostatnie zadanie mi zostało: w trójkącie równoramiennym o podstawie 6 wpisano kolo o r=2 oblicz
dl. ramienia i wysokość. proszę o skazówkę bo nie wiem czy to w ogolę da się rozwiązać.
7 mar 22:41
Basia:
środek okręgu opisanego na wielokącie to punkt przecięcia symetralnych jego boków;
jeżeli trapez nie jest równoramienny to symetralne podstaw są dwiema różnymi prostymi
równoległymi ⇒ nie przecinają się ⇒ nie da się na tym trapezie opisać okręgu
7 mar 22:44
MONIA: Dzięki wszystkim za pomoc.
7 mar 22:50
Basia:
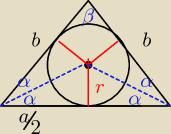
r=2
a=6
wylicz teraz sinα i cosα z układu równań
sin
2α+cos
2α=1
a potem
sin2α=2sinαcosα
cos2α=cos
2α−sin
α
β=180−4α
sinβ=sin4α=2*sin2α*cos2α
z tw.sinusów
z tego wyliczysz b
możliwe, że jest prostszy sposób
7 mar 22:56
 |AC|=a
|BC|=b
|AB|=c
c=a−r+b−r
c=a+b−2r
2r=a+b−c
|AC|=a
|BC|=b
|AB|=c
c=a−r+b−r
c=a+b−2r
2r=a+b−c
 2x+2y+2r = a+b+c
2(x+y)+2r=a+b+c
2c+2r=a+b+c
2r=a+b−c
2x+2y+2r = a+b+c
2(x+y)+2r=a+b+c
2c+2r=a+b+c
2r=a+b−c
 chodzi Ci o to czy w taki czworokąt można wpisać okrąg
warunkiem takiego stanu rzeczy jest aby przeciwległe boki takiego czworokata były sobie równe
czyli a+c=b+d
zakładamy u nas
a=a
b=a+1
c=a+2
d=a+3
otrzymujemy
a=a+2
a+1=a+3
niestety taki układ nie będzie miał rozwiązania w N, czyli takie czworokąt nie istnieje
chodzi Ci o to czy w taki czworokąt można wpisać okrąg
warunkiem takiego stanu rzeczy jest aby przeciwległe boki takiego czworokata były sobie równe
czyli a+c=b+d
zakładamy u nas
a=a
b=a+1
c=a+2
d=a+3
otrzymujemy
a=a+2
a+1=a+3
niestety taki układ nie będzie miał rozwiązania w N, czyli takie czworokąt nie istnieje
 r=2
a=6
r=2
a=6