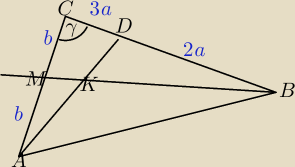
Planimetria - zadanie ze środkową w trójkącie dowolnym Althea: W trójkącie ABC punkt D leżący na boku BC dzieli ten bok na dwa odcinki BD i DC tak, że |BD|DC|=2:3. Odcinek AD przecina środkową BM w punkcie K. Wyznacz stosunek długości odcinków MK i KB. (Liceum) Wyliczyłam niby, że: P_ABC = 5ab sinγ P_ACD = 3ab sinγ

	5
PCBM =		ab sinγ
	2

	5
PABM =		ab sinγ
	2

P_ADB = 2ab sinγ Oraz próbowałam coś dziubać z twierdzeniem cosinusów w trójkątach ABC, ACD i CMB, ale nic z tego. W żaden sposób nie mogę nic wyznaczyć jeśli chodzi o trójkąty KAM i AKB. Ktoś byłby w stanie dopomóc?

Mila:

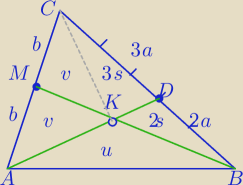
	MK		PΔAMK		v
1)		=		=
	KB		PΔABK		u

Małymi literami oznaczone odpowiednio pola Δ 2) MB− środkowa ΔABC: v+u=v+5s⇔u=5s

u+2s		2		7s		2
	=		⇔		=
2v+3s		3		2v+3s		3

	15s
v=
	4

2)

v		15s   4		3
	=		=
u		5s		4

II sposób Z Tw. Menelausa: ΔCMB przecięto prostą AD:

2a		2b		MK
	*		*		=1⇔
3a		1b		KB

MK		3
	=
KB		4

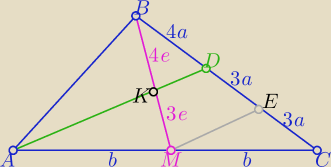Eta: Dwa razy z tw. Talesa

	|MK|		3
		=
	|KB|		4

========== i po ptokach