zadanie dziwne kicia: uzasadnij rownosc przekatnych w prostokacie i rownosc ich polowek:(

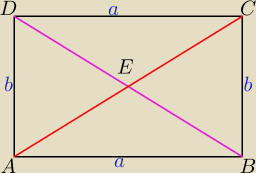
Althea: Nie wiem, jaki poziom (SP, LO? która klasa?), ale równość przekątnych w prostokącie można uzasadnić twierdzeniem Pitagorasa: |AB|²+|AD|²=|BD|² a²+b²=|BD|² |AC|²+|BC|²=|AC|² a²+b²=|AC|² Zatem: |BD|² = |AC|² = a² + b² A jeśli chodzi o połówki − jeśli w treści zadania dosłownie pada słowo połówki, to można to wszystko pomnożyć przez 1/2. Jeśli chodzi o udowodnienie, że |AE|=|DE|=|CE|=|BE|... to nie mam pomysłu.