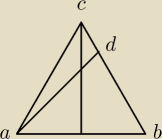 Na boku BC trojkata rownobocznego ABC wybrano taki punkt D, ze pole trojkata ABD jest rowne
6√3
i jest dwa razy większa od pola trojkata ADC. Oblicz dlugosc odcinka AD.
PΔabd=6√3
PΔadc=3√3
PΔabd+PΔadc=9√3=PΔabc
PΔabc=(a2√3)/4=9√3
a=6
dalej utknąłem...
Na boku BC trojkata rownobocznego ABC wybrano taki punkt D, ze pole trojkata ABD jest rowne
6√3
i jest dwa razy większa od pola trojkata ADC. Oblicz dlugosc odcinka AD.
PΔabd=6√3
PΔadc=3√3
PΔabd+PΔadc=9√3=PΔabc
PΔabc=(a2√3)/4=9√3
a=6
dalej utknąłem...
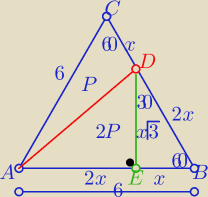
| 3x*x√3 | ||
P(ABD)=2P= 6√3 i 2P= | ||
| 2 |