help KamiL: Jaka jest najwie֒ksza liczba punktow, ktore mozna umiescic w trojka֒cie rownobocznym o boku 2 w taki sposob, by odleglosc dowolnych dwoch nie byla mniejsza niz 1.

wredulus_pospolitus: pytanie −−− czy potrzebujesz tylko odpowiedzieć ... czy może znasz odpowiedź, ale nie wiesz jak to udowodnić

wredulus_pospolitus: I czy 'w trójkącie' oznacza wewnątrz trójkąta, czy boki tegoż trójkąta także się wliczają (to akurat zmieni odpowiedź)

KamiL: Nie znam odpowiedzi i nie wiem jka to udowodnić:( w trojkacie oznacza tylko wewnątrz

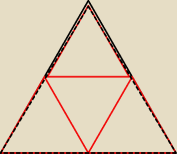
wredulus_pospolitus: Zatem wskazówka: Spójrz na to, że taki trójkąt można podzielić na cztery trójkąty równoboczne o boku równym 1. Jeżeli w którymś z tych mniejszych trójkątów miałbyś dwa punkty, to NA PEWNO będziesz miał je w odległości mniejszej niż 1 od siebie. Związku z tym liczba punktów nie może być większa niż liczba tych trójkątów, czyli nie może być większa od 4. Teraz wystarczy więc tylko pokazać takie ułożenie punktów (spełniające warunki zadania), aby były to cztery punkty.

kerajs: Inaczej: Z punktów bardzo bliskich wierzchołkom zataczasz łuki o promieniu 1. Obszar trójkąta poza tymi łukami jest mniejszy niż trójkąt równoboczny o boku 1 więc w nim może być tylko jeden punkt spełniający warunki zadania, a stąd odpowiedź wskazana przez wredulusa.

KamiL: Czyli ostatecznie 4 punkty (jeden punkt na przecięciu wysokości, 3 na wysokościach)

wredulus_pospolitus: przykładowo ... mogą być w trochę innych miejscach. Istotne jest, że 5'tego nie zmieścisz.

KamiL: W jakich na przykład?

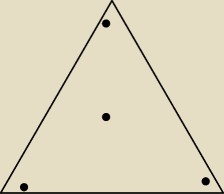
wredulus_pospolitus: np. tak ... czyli 'w pobliżu' miejsc gdzie chciałeś te punkty umieścić.