środek okręgu play: Znając współrzędne trójkąta : A(0,0) B(6,0) C(3,4) wyznacz równanie okręgu wpisanego w ten trójkąt. Wyznaczyłem wszystkie boki AC=5, BC=5, AB=6 oraz wysokość tego trójkąta równoramiennego a

	3
następnie ze wzoru S=rp wyznaczyłem r=		. Do napisania równania okręgu jest potrzebny
	2

jeszcze jego środek, jak go wyznaczyć?

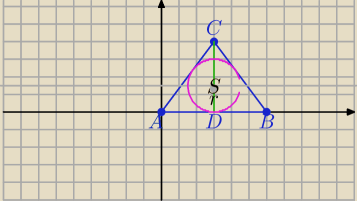
Mila: 1) S=(a,b)− środek okręgu wpisanego w Δ leży w punkcie przecięcia dwusiecznych kątów .

	3
2) Odległość punktu S od boków Δ wynosi r=		( obliczyłeś , nie sprawdzałam)
	2

	3
3) CD− dwusieczna kąta C, |SD|=
	2

	3
S=(3,		)
	2

Pisz równanie okręgu

play: Na podstawie rysunku można co prawda łatwo odczytać, ale bez rysunku skąd od razu wiedziałaś że pierwszą współrzędną będzie x=3 ? bo y to można łatwo wywnioskować z promienia

. : 1) zauważyłeś że jest to trójkąt równoramienny, związku z tym środek okręgu leży na wysokości. Zwiazku z tym znasz już pierwsza współrzędna dla tegoż przypadku (x=3). 2) wyznaczyłeś promień okręgu, związku z tym wystarczy sprawdzić jaki punkt na wysokości jest oddalony o 'r' od podstawy (co też łatwo w tym konkretnym przypadku zrobić)

play: Okej dzięki bardzo