Równania trygonometryczne Vzy: Wyznacz rozwiązania równania 2sinx + √2 = √2cosx + sin2x Po przekształceniu wyszło mi coś takiego: cosx = 1 i wtedy x=0

	√2		π
sinx= −		i tutaj ze wzorów obliczyłam że dla k=0 wychodzi −		ale w odpowiedziach
	2		4

	3
jest jeszcze −		π, mógłby mi ktoś rozpisać i wytłumaczyć jak to ma być poprawnie
	4

rozwiązane? Z góry wielkie dzięki!

Mieszko I: na jedną stronę i przed nawias

Vzy: Tak, już to przekształciłam, mam problem przy samym końcu z wyznaczeniem x

Mieszko I: To pokaż swoje rozwiązanie

Vzy: 2 sinx + √2 = √2 cosx + 2 sinx cosx 2 sinx (1 − cosx) + √2(1 − cosx) = 0 (1− cosx)(2sinx + √2) = 0 cosx=1 2sinx + √2=0

	√2
x=0 sinx= −
	2

	π
x0= −
	4

Vzy: Coś takiego mam i teraz nie wiem jak dalej to obliczyć. Próbuję podstawiać pod wzór x₀ + 2kπ i π − x₀ + 2kπ ale nie wychodzi mi −3/4π

chichi:

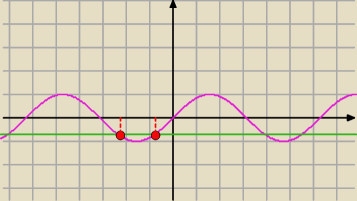
	√2
namierzyłeś tylko jedno z rozwiązań równania sin(x) = −
	2

Vzy: chichi bardzo dziękuję za rozrysowane a mógłbyś mi jeszcze pomóc z wyliczeniem tego ze wzorów bez używania wykresu? Bo jeśli się nie mylę można to zrobić właśnie na dwa sposoby, a

	√2
ja mam problem z rysowaniem tych wykresów jak są takie ułamki jak np. właśnie
	2

. : Wskazowka: sin x = sin(−π − x)