czworokąty i koła fabian: W trójkącie ABC dwusieczne kątów przy wierzchołkach B i C przecinają przeciwległe boki tego trójkąta w punktach odpowiednio D, E, same zaś przecinają się w punkcie O. Ponadto na czworokącie ADOE można opisać okrąg. Wykaż, że |<BAC| = |<OBC|+|<OCB|. (< to znaczek kąta jakby co)

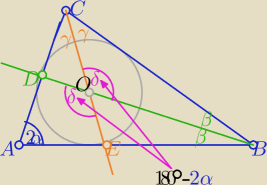
Eta: 1/ przejrzysty rys, zgodny z treścią zadania 2/z warunku wpisania okręgu w czworokąt δ= 180^o−2α to w ΔBOC : 180⁻2α+γ+β=180^o i mamy tezę....

Eta: poprawiam zapis 2/ z warunku wpisania czworokąta w okrąg

fabian: dobrze i co dalej z tą teza bo myślę i nie wiem o co chodzi

. : Piszesz: 180 − 2α + β + γ = 180 − − > 2α = β + γ C. N. W. Koniec

. : Pytanie kluczowe − − czy wiesz dlaczego δ = 180 − 2α

fabian: tak wiem dlaczego dziękuję za pomoc