Geometria Analityczna Karol: Wyznacz równanie okręgu przechodzącego przez punkty A = (− 5,3) i B = (0,6) , którego środek leży na prostej o równaniu x− 3y + 1 = 0 . Jestem na etapie, żę |AS|²=|AB|² i jak liczę długość |AS|² podstawiając za y 1/3x+3 wychodzi mi ujemna delta i nie wiem co dalej.

ABC: nie lepiej napisać równanie cięciwy AB , puścić do niej prostopadłą i przeciąć z daną prostą ?

. : ABC − czyli środkowa odcinka

ABC: no symetralną , sądziłem że każdy nauczyciel uczy tej metody ale może byłem zbytnim optymistą

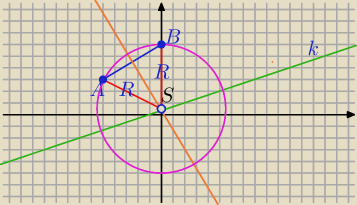
Mila: k: x− 3y + 1 = 0 1) Symetralna AB: A=(− 5,3) B = (0,6) (x+5)²+(y−3)²=x²+(y−6)²

	5		1
s: y=−		x+
	3		3

dokończ

Jolanta: Czy taki wzór jest w wybranych wzorach matematycznych dla maturzystów ?

Eta: O jaki Jolu wzór pytasz ?

Jolanta: Pytam o to co napisał ABC równanie cieciwy

Jolanta: Cięciwa leży na prostej przechodzącej przez A i B Czyli napisalabym równanie prostej przechodzącej przez punkt A i B Otrzymam współczynnik kierunkowy a Policzylabym srodek odcinka AB Przechodzi przez niego symetralna ,której współczynnik kierunkowy= −1/a W miejscu gdzie podana prosta przecina się z symetralna leży środek okregu