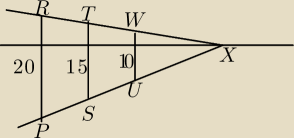
Tw. Talesa Anna: Kolumny przedstawione na rysunku w rzeczywistości mają równe wysokości. Liczby na rysunku oznaczają długości narysowanych odcinków w milimetrach a) Uzasadnij, że w rzeczywistości odległość między kolumnami RP i TS jest inna niż między kolumnami TS i WU. Moje rozwiązanie (nie wiem czy dobre): Z trójkątów podobnych XUW i XST

XW		XT
	=		⇒ 3XW=2XT ⇒ 3XW=2(TW+XW) ⇒ XW=2TW
10		15

Z trójkątów XPR i XST:

XT		15		XW+TW		3
	=		⇒		=		⇒4XW+4TW=3TR⇒4TW=TR
TR		20		TR		4

4TW=TR, co oznacza, że odległości pomiędzy kolumnami PR i ST a ST i UW są różne. b) Przypuśćmy, że przed kolumną oznaczoną na rysunku RP w tej samej linii stoi jeszcze jedna kolumna o tej samej wysokości, ale jej odległość ( w rzeczywistości) od kolumny RP jest taka sama jak odległość między kolumnami RP i TS. Ustal, jaką długość powinien mieć odcinek przedstawiający tę kolumnę na rysunku. I tutaj nie wiem jak rozwiązać

Anna:

	XT		3
Jednak jest błąd w pkcie a, bo z trójkątów XPR i XST wychodzi		=		, co prowadzi do
	XR		4

TW=TR

wredulus_pospolitus: Skąd masz to zadanie? Trudno udowodnić coś co nie jest prawdą (coś co przeczy chociażby wnioskom z tw. Talesa)

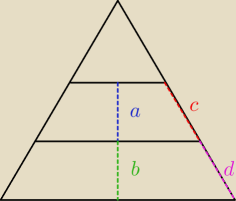wredulus_pospolitus: taka uwaga −−− masz pokazać zależność pomiędzy a i b .... a nie to o pokazałaś czyli pomiędzy c i d