trapez ciezki IWOI: W trapezie prostokątnym dłuższa przekątna ma długość 24 i zawiera się w dwusiecznej kąta ostrego trapezu. Odległość wierzchołka kąta rozwartego trapezu od dłuższej przekątnej wynosi 9. Oblicz pole trapezu. wiem ze tworza sie katy 90−α iα w kacie ADC oraz 180−2α w kacie DCB ale nawet nie mam pomysłu co dalej tutaj zrobic bo chyba nawet nie mozna wpisac okregu w to a twierdzenie cosinusow jest z 3 niewiadomymi

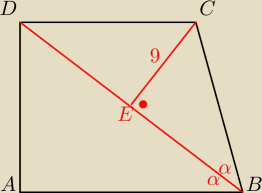
an: Co powiesz o ∡EDC

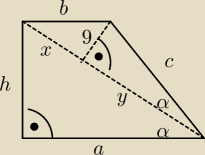
wredulus_pospolitus: Mamy 6 niewiadomych ... warto by było znaleźć 6 równań. 1) x+y = 24 2) a² + h² = 24² 3) x² + 9² = b² 4) y² + 9² = c² 5) (a−b)² + h² = c²

	9		h
6) z podobieństwa trójkątów (patrz podobieństwo typu KKK) mamy:		=
	c		24

Trochę zabawy będzie, ale da się przerobić

ite: niewiadomych jest mniej, na rysunku z 17:40 x=y i b=c, więc warto to wykorzystać

IWOI: tak an zauwazylem ze jest kat prosty od dlugosci bo to definicja odleglosci, lecz mialem problem z wyznaczeniem prawdlowo podobienstwa, ale juz sobie chyba poradze dziekuje

an: kąt ADC jest prosty to wynika z treści, mnie chodzi oto, że ∡EDC=α bo ∡ADB=90^o−α

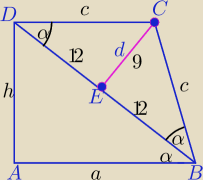
Iryt: c=15 dalej dwa razy podobieństwo albo inaczej.

an: To są jak widać na 17:34 trójkąty podobne do Pitagorajskiego 3:4:5 czyli można i tak

	1		3		4		1
P=		*		*24 *		*24+		*9*24= 246,24
	2		5		5		2

IWOI: a no to logiczne ja to mialem problem z zrozumieniem jak mam zrobic to prodobienstwo mimo ze nawet widzialem ten kat lecz juz sie udalo dziekuje za pomoc

Adam: Wytłumaczy mi ktoś czemu ta prosta dzieli podstawe DB na pół?

Aruseq: Z równości kątów przy D i B − trójkąt BCD jest równoramienny

Adam: ale czemu kąt D jest równy kątowi B?, w sensie z czego wynika, że ten trójkąt jest równoramienny

Aruseq: Kąty naprzemianległe