help adam: wyznacz wszystkie wartości parametru m dla których wykres funkcji liniowej f(x)=mx+4 ma co najmniej jeden punkt wspolny z kwadratem ABCD ,ktorego wierzchołki maja wspolrzedne A(3.1) B(9.3) C(7.9) D(1.7)

. : Bez względu na współczynnik m, znasz współrzędne jednego punktu dla tejże prostej. Wyznacz sobie cztery proste (dla pewności) podstawiając jako druga współrzędna kolejne wierzchołki tegoż kwadratu. Na podstawie uzyskanych wyników podaj odpowiedź.

adam: nie zbyt to rozumiem mozna jakies rozwiazanie albo innaczej wytlumaczyc?

adam: Czy ma sens ze stwierdze ze punkt G(0.4) nalezy do funkcji f(x)=mx+4 i uznam ze 1 punkt jaki ta prosta bedzie miala wspolny z kwadratem idac zgodnie z ruchem wskazówek zegara to punkt D(1.7) oblicze dla tych 2 punktow m po wyliczeniach wychodzi ze m=3 ostatnim punktem wspolnym bedzie punkt A(3.1) wyznacze prosta przechodząca przez te 2 punkty i wychodzi ze m=−1 jako iż kazda prosta miedzy wyznaczonymi ma minimum jeden punkt wspolny z kwadratem to m nalezy od (−1 do 3)? jest to w miare dobre rozwiazanie czy raczej zbyt śliskie i na przyklad na maturze by mi nie dali fulla punktow

wredulus_pospolitus: i to dokładnie było podane o 17:41, tylko tam jeszcze była sugestia by sprawdzić pozostałe dwa wierzchołki kwadratu (B i C) ... tak dla pewności

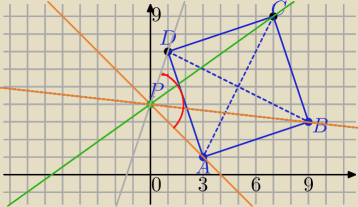
Mila: A=(3,1), B=(9,3), C=(7,9) D=(1,7) P=(0,4) f(x)=mx+4 f(3)=1⇔3m+4=1⇔m=−1 PA: y=−x+4 f(9)=3⇔9m+4=3⇔9m=−1

	1
PB: y=−		x+4
	9

	1
m∊<−1,−		>
	9

	5
PC: f(7)=9⇔ m=
	7

	5
PC: y=		x+4
	7

PD: y=3x+4 m∊<−1,3>

adam: a co jezeli funkcja f(x) miala by rownanie np, f(x)=mx+3m wtedy nie znamy punktu zadnego prostej co wtedy?

an: w podanym równaniu f(x)=mx+3m prosta przechodzi przez punkt (−3,0), a więc nie ma problemu

adam: Aha faktycznie ze tez sam na cos takiego nie wpadłem Dzieki wielkie. mam ostatnie pytanie co jezeli bym mial 2 proste np y=mx+3m i y= (m+2)x−m i pytanie dla jakiego m proste maja punkt przeciecia w tym kwadracie

adam: Albo jeszcze jedno np prosta y= mx−m² i pytanie dla jakiego m ta prosta ma punkt wspolny z kwadratem

wredulus_pospolitus: odnośnie drugiej: y = mx − m² −−−> y = m(x−m) czyli jednym z punktów (który nie będzie już stały bez względu na m) będzie (m, 0) reszta jak w poprzednich przypadkach

wredulus_pospolitus: Jeśli chodzi o to czy się dwie proste przetną wewnątrz kwadratu. zauważmy, najpierw że mamy: mx + 3m = (m+2)x − m −−−> 4m = 2x −−−> x = 2m −−−> y = 2m² + 3m −−−> (2m ; 2m² + 3m) będzie punktem przecięcia się tych dwóch prostych. Sprawdź dla jakich 'm' tenże punkt będzie wewnątrz kwadratu