Geometria płaska
Kochones:
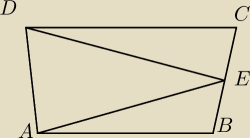
Dany jest czworokąt ABCD. , w którym AB||CD. Na boku BC wybrano taki punkt E, że |EC=|CD| i
|EB|=|BA|.
Wykaż, że kąt AED jest prosty.
|BAE|=|AEB|=α
|EDC|=|ECD|=β
|AED|=180−(α+β)
W mojej próbie należy dojść do tego, że α+β=90. Proszę o pomoc.
7 kwi 14:40
an:
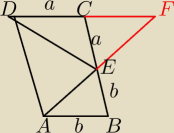
co można powiedzieć o ∡CEF oraz ∡CFE i △DEF
7 kwi 15:42
Kochones: Miara kąta CEF jest taka sama jak miara kąta AEB czyli równa α (kąty wierzchołkowe).
Miara kąta CFE jest taka sama jak miara kąta BAE (z kątów odpowiadających).
Miara kąta ECF jest taka sama jak miara kąta ABE (z kątów odpowiadających).
Zatem trójkąt CEF jest podobny do trójkąta ABE z własności kąt−kąt−kąt.
A co powiedzieć o trójkącie DEF to nie mogę tego dostrzec.
7 kwi 16:08
Kochones: Jeszcze można stwierdzić, że |CF|=a
7 kwi 16:08
an: Chodzi o sumę kątów kątów ΔDEF
7 kwi 16:15
Kochones: No jasne
2α+2β=180
α+β=90
Dziękuję za pomoc!
7 kwi 16:21
 Dany jest czworokąt ABCD. , w którym AB||CD. Na boku BC wybrano taki punkt E, że |EC=|CD| i
|EB|=|BA|.
Wykaż, że kąt AED jest prosty.
|BAE|=|AEB|=α
|EDC|=|ECD|=β
|AED|=180−(α+β)
W mojej próbie należy dojść do tego, że α+β=90. Proszę o pomoc.
Dany jest czworokąt ABCD. , w którym AB||CD. Na boku BC wybrano taki punkt E, że |EC=|CD| i
|EB|=|BA|.
Wykaż, że kąt AED jest prosty.
|BAE|=|AEB|=α
|EDC|=|ECD|=β
|AED|=180−(α+β)
W mojej próbie należy dojść do tego, że α+β=90. Proszę o pomoc.
 co można powiedzieć o ∡CEF oraz ∡CFE i △DEF
co można powiedzieć o ∡CEF oraz ∡CFE i △DEF