Długości boków trójkąta są w stosunku 2 : 3 : 4
uczen: Hejka potrzebuje pomocy z tym zadankiem
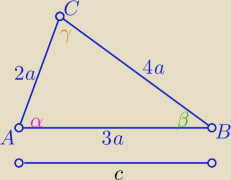
Długości boków trójkąta są w stosunku 2 : 3 : 4. Oblicz wartość wyrażenia
1/tgα + 1/tgβ
gdzie α oznacza największy, a β najmniejszy kąt tego trójkąta.
6 kwi 20:04
wredulus_pospolitus:
ok ... a co z trygonometrii już miałeś? Jakie wzory? Jakie twierdzenia?
6 kwi 20:09
uczen: jestem maturzysta wiec, cale liceum
6 kwi 20:39
6 kwi 21:07
a7:
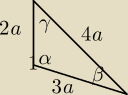
1. 1/tgα+1/tgβ= cosα/sinα +cosB/sinB=...= sinγ/(sinα*sinβ)
2. z tw sinusów
3a/sinα=2a/sinB czyli sinα=3/2sinB
3. z tw sinusów
3a/sinγ=2a/sinB czyli sinB=2/3sinγ
4. czyli sinγ/(sinα*sinB)=3/(2sinγ)
5. z tw cosinusów
(3a)
2=(2a)
2+(4a)
2−2*2a*4acosγ czyli cosγ=11/16 czyli sinγ=
√135/256=3
√15/16
czyli 3/(2sinγ)=8
√15/15
6 kwi 21:09
Eta:
Jest taki ładny wzorek
| | 1 | | 1 | | 9a2 | |
to W= |
| + |
| = |
| |
| | tgα | | tgβ | | 2P | |
ze wzoru Herona
..............
==========
6 kwi 21:16
a7: no widać, że przynajmniej {15} się u mnie zgadza, pza tym musiały się wkraść chohcliki
obliczeniowe, przepraszam, ale metoda chyba dobra
6 kwi 21:21
a7: Poprawiam
2. z tw.sinusów 4a/sinα=2a/sinB czyli sinα=2sinB
3 z tw. sinusów 3a/sinγ=2a/sinB czyli sinB=2/3sinY
4 czyli sinγ/(sinαsinB)=sinγ/(2sin
2B)−sinγ/ (2*4/9*sin
2γ)=9/(8sinγ)= 9/8*16/
√135=2
√15/5

6 kwi 21:56
Eta:

6 kwi 21:59
Uczeń : Dzieki wielkie
6 kwi 22:09
 https://zadania.info/d449/3906670
https://zadania.info/d449/3906670
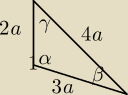 1. 1/tgα+1/tgβ= cosα/sinα +cosB/sinB=...= sinγ/(sinα*sinβ)
2. z tw sinusów
3a/sinα=2a/sinB czyli sinα=3/2sinB
3. z tw sinusów
3a/sinγ=2a/sinB czyli sinB=2/3sinγ
4. czyli sinγ/(sinα*sinB)=3/(2sinγ)
5. z tw cosinusów
(3a)2=(2a)2+(4a)2−2*2a*4acosγ czyli cosγ=11/16 czyli sinγ=√135/256=3√15/16
czyli 3/(2sinγ)=8√15/15
1. 1/tgα+1/tgβ= cosα/sinα +cosB/sinB=...= sinγ/(sinα*sinβ)
2. z tw sinusów
3a/sinα=2a/sinB czyli sinα=3/2sinB
3. z tw sinusów
3a/sinγ=2a/sinB czyli sinB=2/3sinγ
4. czyli sinγ/(sinα*sinB)=3/(2sinγ)
5. z tw cosinusów
(3a)2=(2a)2+(4a)2−2*2a*4acosγ czyli cosγ=11/16 czyli sinγ=√135/256=3√15/16
czyli 3/(2sinγ)=8√15/15
 Jest taki ładny wzorek
Jest taki ładny wzorek

