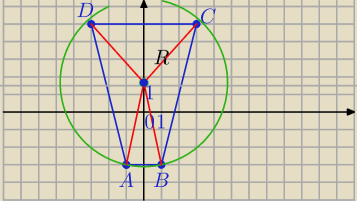
okrag na trapezie a: wyznacz rownanie okregu opisanego na czworokacie abcd, jest to trapez rownoramienny a −1 , −3 b 1, −3 c 3,5 d −3,5

getin: oś Y jest osią symetrii tego trapezu, środek okręgu musi się znajdować na tej osi, zatem S = (0,y). Musi być też spełniony warunek |SB| = |SC| bo każdy z tych odcinków SB i SC musi być promieniem R tego okręgu opisanego |SB| = √(1−0)² + (−3−y)² = √1+9+6y+y² = √y²+6y+10 |SC| = √(3−0))² + (5−y)² = √9+25−10y+y² = √y²−10y+34 |SB| = |SC| wtedy, gdy √y²+6y+10 = √y²−10y+34 y²+6y+10 = y²−10y+34 16y = 24

	3
y =
	2

	3
S = (0,		)
	2

promień R = |SC| = √y²−10y+34 = √(3/2)²−10*3/2+34 = √2,25−15+34 = √21,25

	3
Równanie okręgu o środku S = (0,		) i promieniu R = √21,25 ma postać
	2

	3
x2 + (y−		)2 = 21,25
	2

Mila: B=(1, −3), C=( 3,5) II sposób Symetralna BC: (zbiór wszystkich punktów P(x,y) jednakowo odległych od końców odcinka BC) (x−1)²+(y+3)²=(x−3)²+(y−5)² s: 4x+16y−24=0 Punkt przecięcia OY i s x=0

	3
16y=24, y=
	2

	3
S=(0,		)
	2

dalej j.w.