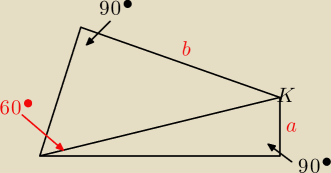
 Do obszaru kąta ostrego o mierze 60deg należy punkt K , którego odległości od ramion kąta są
równe a i b . Oblicz odległość punktu K od wierzchołka kąta.
Do obszaru kąta ostrego o mierze 60deg należy punkt K , którego odległości od ramion kąta są
równe a i b . Oblicz odległość punktu K od wierzchołka kąta.
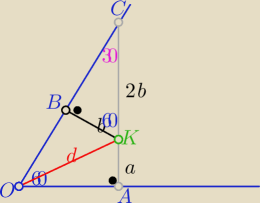 Jeden ze sposobów
Wykorzystując własności trójkatów "ekierkowych" o kątach ostrych 60o i 30o
Jeden ze sposobów
Wykorzystując własności trójkatów "ekierkowych" o kątach ostrych 60o i 30o
| 2b+a | ||
|OA|= | *√3 | |
| 3 |
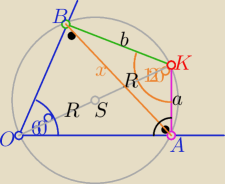 z tw. cosinusóww ΔABK
x2= a2+b2+ab
i z tw. sinusów w ΔABO , |OK|=2R
z tw. cosinusóww ΔABK
x2= a2+b2+ab
i z tw. sinusów w ΔABO , |OK|=2R
| x | ||
|OK|=2R= | =............. | |
| sin60o |
| 2√a2+ab+b2 | ||
|OK|= | ||
| 3 |
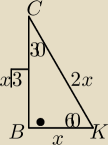
| 2√3√a2+b2+ab | ||
|OK|= | ||
| 3 |