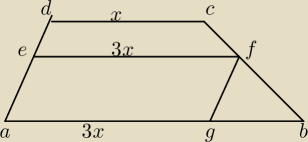
 Dany jest trapez
ABCD, gdzie AB∥CD . Na ramionach AD i BC obrano odpowiednio punkty E i F takie, że EF∥AB.
Na podstawie AB obrano punkt G taki, że czworokąt AGFE jest równoległobokiem. Pole czworokąta
EFCD jest równe 18, pole trójkąta GBF jest równe 4. Wyznacz pole trapezu ABCD, jeśli wiadomo,
ze
∥EF=3*CD
Dany jest trapez
ABCD, gdzie AB∥CD . Na ramionach AD i BC obrano odpowiednio punkty E i F takie, że EF∥AB.
Na podstawie AB obrano punkt G taki, że czworokąt AGFE jest równoległobokiem. Pole czworokąta
EFCD jest równe 18, pole trójkąta GBF jest równe 4. Wyznacz pole trapezu ABCD, jeśli wiadomo,
ze
∥EF=3*CD
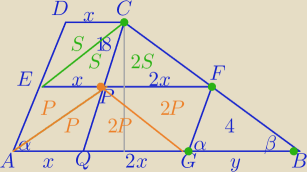 Literami S i P oznaczyłam pola odpowiednich Δ.
1)
ΔEPC i ΔCPF mają taką samą wysokość
4S=18⇔2S=9
2)ΔCPF∼ΔGBF
Literami S i P oznaczyłam pola odpowiednich Δ.
1)
ΔEPC i ΔCPF mają taką samą wysokość
4S=18⇔2S=9
2)ΔCPF∼ΔGBF
| 9 | |
=k2 | |
| 4 |
| 3 | 2x | 3 | ||||
k= | ⇒ | = | ||||
| 2 | y | 2 |
| 3 | ||
x= | y | |
| 4 |
| 3 | ||
P= | *PΔGBD=3⇒PΔQGP=2P⇔ | |
| 4 |
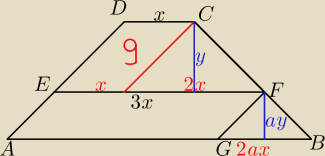 P=40
P=40