geometria beata: Cześć mam problem z zadaniem. Wiem, że trzeba użyć twierdzenia talesa, ale nie wiem do jakich trójkątów. Podstawy czterech przystających trójkątów równobocznych leżą na jednej prostej. Wierzchołek pierwszego trójkąta połączono odcinkiem z wierzchołkiem czwartego trójkąta (patrz rysunek). Oblicz stosunek pola zacieniowanego do pola jednego trójkąta równobocznego

getin: Oznaczmy bok jednego trójkąta równobocznego przez 12a Z tw. Talesa, dwa górne boki zacieniowanych trójkątów to odpowiednio: − dla pierwszego od lewej (największego) zacieniowanego trójkąta to 12a oraz 9a − dla drugiego to 8a i 6a − dla trzeciego to 4a i 3a −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Wykorzystaj wzór na pole trójkąta z sinusem aby znaleźć szukaną proporcję (kąt między dwoma bokami trójkąta równobocznego wynosi 60^o)

	7
Odp. to
	6

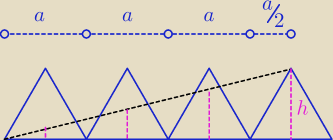ite: Można też skorzystać z tw. Talesa dla wysokości i liczyć pola zacieniowanych trójkątów odejmując pola niezacieniowane.

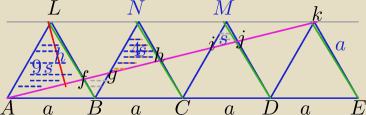Mila: P_ΔABL=P 1) Ramiona kąta KAE przecięto prostymi równoległymi (zielonymi) Z tw.Talesa : |AF|=|FH|=|HJ|=JK| 2) Ramiona kąta KAE przecięto prostymi równoległym (Niebieskimi): |AG|=|GI|=IIK| 3) Z (1 i 2) |AG|=|AF|+|FG|=|IJ|+|JK|⇒|FG|=|IJ| ΔFBG≡ΔIJM ΔGHN≡ΔHIC⇒|GH|=HI| ΔAFL≡ΔJDK P_ΔAKL=3P

	ID		a		3		1
4) Z podobieństwa odpowiednich Δ: (		=		, ID|=		a, |MJ|=		a )
	3a		4a		4		4

	1		2		3
|MJI=		a , NH=		a, F=		a
	4		4		4

Pola zacieniowanych Δ: s,4s,9s 5) Suma pól zacieniowanych: P_zΔ=14s

	1
PΔAKL=3P=		*|AK|*h
	2

	1
3P=		*4*|AF|*h
	2

	1
3P=4*(		*|AF|*h)
	2

3P=4*9s P=12s

14s		7
	=
12s		6

===========