Dowód - planimetria - rozszerzenie Karolina: Cześć, nie mam pomysłu na taki dowód: w trójkącie ABC kąt BAC jest dwa razy większy od kąta ABC. Wysokość opuszczona z wierzchołka C przecina bok AB w punkcie D. Wykaż, że |BD|−|AD|=|AC|

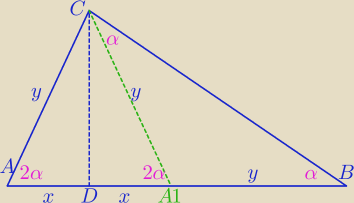
ite: Tezę można zapisać równoważnie: |BD|=|AC|+|AD| a z uwzględnieniem oznaczeń z rysunku |BD|=x+y Czy już widzisz, jak to wyakzać?

wmboczek: CD=ACsin2α=BDtgα tgα(AC2sos²α−BD)=0 tgα(AC2sos²α−AC +AC −BD)=0 tgα(ACsos2α−BD+AC)=0 tgα(AD+AC−BD)=0

Karolina: To było takie proste. Nie zauwazyłam tych trójkątów równoramiennych. Dziękuję!