proszę o rozwiązanie anna: W romb o boku a wpisano dwa okręgi w ten sposób, że okręgi te są styczne zewnętrznie i każdy z nich jest styczny do dwóch sąsiednich boków rombu przecinających się pod kątem ostrym α Udowodnij, że suma promieni tych okręgów jest równa ( 2asinα) / (2+√2 −2 cosα)

ite: Czy komuś wyszedł taki wynik? Uporczywie dostaję inny mianownik.

an: Chyba chodzi

2asinα
2+√2−2cosα

ite: dokładnie tak + wreszcie informację o kącie ostrym można wykorzystać

anna: przepraszam bardzo rzeczywiście jest tak jak napisał an: 2 kwi14:01 tekst był niewyraźnie napisany

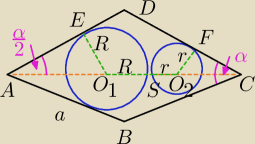
ite: Moje próby narysowania przyzwoicie wyglądającego rysunku wypadły słabo, więc wstawiam dodatkowo rysunek z geogebry: https://zapodaj.net/74e30c3686539.jpg.html Spróbuj zacząć od policzenia długości odcinka |AC| za pomocą cosinusa kąta <EAS. Potem zapisz ten sam odcinek jako sumę długości |AO₁| (policzonej z sinusa kąta <EAS), obu promieni i odcinka |CO₂| (też policzonego z sinusa kąta <EAS). W razie wątpliwości pytaj.