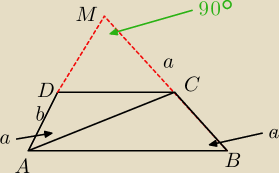
planimetria silnia: W trapezie ABCD boki nierównoległe AD i BC zawierają się w prostych prostopadłych. Oblicz pole trapezu, mając dane |AD | = a oraz |∡ABC | = |∡DAC | = α Literą a oznaczyłem kąt alfa przy wierzchołku A i wierzchołku B, korzystając z AB || CD, ∡DCM = α. Dalej nie wiem jak to ruszyć.

. : Spodziewam się ze będzie konieczność zabawy z tw. Pitagorasa, tw. Talesa, podobieństwem trójkątów.

an: pole ΔDAC +pole ΔACB z proporcji do ΔDAC

	a2
P=
	2cos2α tgα

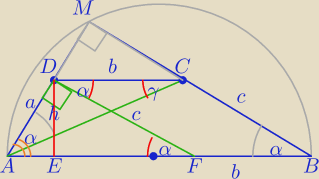
Mila: 1) W ΔMAB: ∡A=90^o−α 2) W ΔAED: h=a*sin(90−α)=a*cosα ======== W ΔADF:

	a
sinα=
	AF

	a
|AF|=
	sinα

========= 3) W ΔADC: α+90^o+α+γ=180^o γ=90^o−2α Z tw. sinusów:

b		a
	=
sinα		sinγ

b*sin(90−2α)=a*sinα

	a*sinα
b=
	cos(2α)

=========== 4) AB: |AB|=|AF|+b

	1		a		a*sinα
5) PABCD=		*(		+2*		)*a*cosα
	2		sinα		cos(2α)

dokończ

Eta: https://zadania.info/d633/8982359 tu masz jeszcze trzy sposoby rozwiązania zadania

silnia: Tak, ale zastanawialem sie dlaczego ∡CAB = ∡DAB − ∡DAC = 90 ∘ − 2 α.

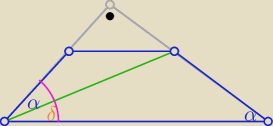
Eta: α+δ= 90^o−α ⇒ δ=90^o−2α czy teraz jasne ?

Mila: 20:31 ∡CAB =∡γ , a kąt γ obliczyłam.

Mila: Piszemy, wyjaśniamy i nie wiadomo, czy autor zadania to czyta.

an: MA=m; MB=n⇒ n=m*tgα

m		m
	=AC=
sin(90o−α)		sin(90o−2α)

an: Niezamierzony wpis spadł jakiś fragment