Oblicz pole obszaru zawartego między krzywymi Bdss: y²=x³ , y²=2−x Próbowałam z 2* ∫₀ ¹ √(2−x) − √(x³) Ale wychodzi mi inny wynik niż w podręczniku (odpowiedź: ³²₁₅)

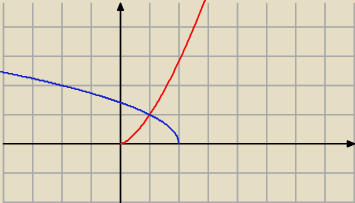
wredulus_pospolitus: ale o który obszar chodzi

Bdss: y jest podniesione do kwadratu, więc jest moduł. Czyli te wykresy są odbite symetrycznie względem osi Ox, przy czym x należy do przedziału <0,2>

jc: Narysuj oś y poziomo, a oś x pionowo. Dostaniesz całkę ∫₋₁¹ (2−y²−y^2/3) dy = [2y−y³ /3 − 3/5 y^5/3]₋₁¹ = 2(2− 1/3 − 3/5) = 32/25