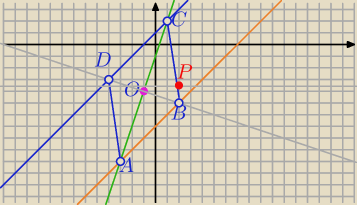
proszę o rozwiązanie anna: W kartezjańskim układzie współrzędnych dany jest romb ABCD , którego bok CD i przekątna AC są zawarte w prostych o równaniach y − x − 1 = 0 i y − 3x + 1 = 0 odpowiednio. Promień okręgu wpisanego w romb ABCD jest równy 2√2 a środek tego okręgu leży poniżej osi Ox . Oblicz współrzędne punktu styczności okręgu wpisanego w romb ABCD z jego bokiem BC . obliczyłam współrzędne punktu C = (1 ; 2) niestety nie wiem jak dalej rozwiązać

ite: wykorzystaj dwie informacje: 1/ przekątna AC jest osią symetrii tego rombu → to pozwoli wyznaczyć prostą, w której zawiera się bok CB, 2/ wysokość rombu jest równa średnicy okręgu wpisanego czyli taka jest odległość między bokami rombu → to pozwoli wyznaczyć proste zawierające boki AD i AB

anna: zadanie rozwiązałam i mam takie wyniki 1 obliczyłam współrzędne punktu C = (1 ;2) 2 obliczyłam współrzędne punktu przecięcia przekątnych S = (−1 ;−4) 3 równanie pr0stej BD y = −¹₃ x − ¹³₃ 4 wierzchołek D =(−4 ;−3) 5 współrzędne wierzchołka B = (2; − 5) 6 współrzędne wierzchołka A = (−3 ; −10) 7 równanie prostej AD y = −7x −31 8 równanie prostej BC y = −7x + 9 9 współrzędne punktu styczności P z prostą BC P = (⁹₅ ; ⁻¹⁸₅) czy te wyniki są poprawne bo nie mam odpowiedzi proszę o sprawdzenie

Mila: y − x − 1 = 0 i y − 3x + 1 = 0 CD : y=x+1 AC: y=3x−1 C=(1,2)− punkt przecięcia prostych 1) h=2r=4√2 − odległość między prostymi równoległymi DC i AB y−x−1=0 AB: y−x+C=0

|C−(−1)|
	=4√2
√12+12

C+1=8 lub C+1=−8 C=7 lub C=−9 y−x+7=0 lub y−x−9=0 AB: y=x−7 lub y=x+9 nie odp. war. zadania 2) Punkt przecięcia Prostej AC i AB x−7=3x−1 −2x=6 x=−3, y=−10 A=(−3,−10) O − środek odcinka AC, C=(1,2) O=(−1,−4) 3) Prostopadła CD przechodząca przez pkt. O

	1		1		2
y=−		x+b i −4=−		*(−1)+b, b=−3
	3		3		3

	1		13
y=−		x−
	3		3

Punkt przecięcia z prostą AB

	1		13
−		x−		=x−7
	3		3

x=2,y=−5 B=(2,−5) 4) prosta BC: C=(1,2) , B=(2,−5) y=−7x+9 Prostopadła do BC i przechodząca przez O. dalej też dobrze

anna: dziękuję bardzo