obliczyć pole pomiędzy krzywymi xyz: y=x² y=1/4 x² y=3 wykres narysowałam i wychodzi mi, że granica jest od −4 do 4 a całke zrobiłam 4−1/4x² vzy mógłby ktos mi napisać jak jets poprawnie

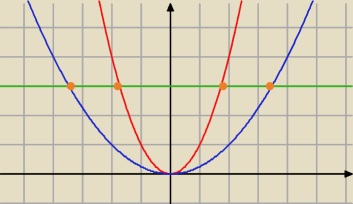
wredulus_pospolitus: źle granice całkowania co oznacza niby ten zapis: 4 − 1/4x² Bo z pewnością miałeś inny zapis w zamyśle

xyz: dobra juz wiem jak, dzieki

xyz: a jak taką całkę ∫e^−IxI

wredulus_pospolitus: to ma byc całka oznaczona czy nieoznaczona

xyz: oznaczona, granica od −nieskończoności do nieskończoności ale nie wiem jak samą całkę obliczyć

wredulus_pospolitus: jako że jest to funkcja parzysta ... wystarczy policzyć ∫₀^+∞ e^−|x| dx = ∫₀^+∞ e^−x dx i wynik przemnożyć przez 2

xyz: ok, a jeszcze mam problem z jednym zadaniem polcenie oblicz pole i krzywe to

	1
y=
	x2(x+1)

y=0 x=1 dla x≥1 graniaca to od 1 do +∞ i wyszło mi lim(−lna−1/a+ln Ia+1I)−(ln1−1+ln2) a−>∞ odp to 1−ln2 i tyle wyjdzie mi z tego 2 nawias, ale z 1 wychodzi mi nieskończonośc

. : Zauwaz ze: −lna + ln(a+1) = ln(1 + 1/a) − − > ln 1 = 0