Planimetria dowodzenie
silnia:
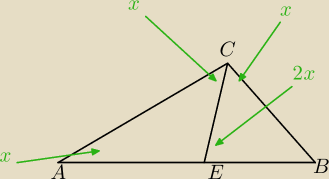
W trójkącie ABC miara kąta ACB jest dwa razy większa od miary kąta CAB . Dwusieczna kąta ACB
dzieli trójkąt ABC na dwa trójkąty. Uzasadnij, że:
a) jest równoramienny
b) jeden z otrzymanych trójkątów jest podobny do trójkąta ABC.
|∡AEC| = 180deg−2x
|∡BEC| = 180deg − (180deg−2x)=2x
a) Ja zrobilbym to tak, ale nie wiem czy moje wnioski i sformulowania wpasowuja sie w klucz, w
dodatku wydaje mi sie, ze uzywam malo matematycznego jezyka.
|∡EAC| = |∡ECA| = x
|∡AEC| = 2x
⇒ trójkąt równoramienny, przy jednym boku występują kąty o tej samej mierze.
b) |∡ABC| = β,
w Δ
ABC mamy kąty: x, 2x, β
w Δ
EBC mamy kąty: x, 2x, β (wspólny)
trójkąty podobne, cecha kąt−kąt−kąt
30 mar 17:43
ite:
Ani zapisane pytanie a/ (z punktu widzenia erotetyki : ) ani podana odpowiedź nie są poprawne.
Nie wiadomo, o co pytamy i nie wiadomo, jaka jest odpowiedź.
30 mar 18:15
silnia: Zatem co nalezy zrobic?
30 mar 19:52
ite:
W punkcie a/ pewnie chodzi o uzasadnienie, że któryś trójkąt jest równoramienny (tego trójkąta
brakuje).
W odpowiedzi powinna pojawić się informacja, że ten trójkąt to ΔAEC, samo wyliczanie kątów to
mało.
W zapisie miary kąta |∡AEC| zginęło180o.
30 mar 20:59
 W trójkącie ABC miara kąta ACB jest dwa razy większa od miary kąta CAB . Dwusieczna kąta ACB
dzieli trójkąt ABC na dwa trójkąty. Uzasadnij, że:
a) jest równoramienny
b) jeden z otrzymanych trójkątów jest podobny do trójkąta ABC.
|∡AEC| = 180deg−2x
|∡BEC| = 180deg − (180deg−2x)=2x
a) Ja zrobilbym to tak, ale nie wiem czy moje wnioski i sformulowania wpasowuja sie w klucz, w
dodatku wydaje mi sie, ze uzywam malo matematycznego jezyka.
|∡EAC| = |∡ECA| = x
|∡AEC| = 2x
⇒ trójkąt równoramienny, przy jednym boku występują kąty o tej samej mierze.
b) |∡ABC| = β,
w ΔABC mamy kąty: x, 2x, β
w ΔEBC mamy kąty: x, 2x, β (wspólny)
trójkąty podobne, cecha kąt−kąt−kąt
W trójkącie ABC miara kąta ACB jest dwa razy większa od miary kąta CAB . Dwusieczna kąta ACB
dzieli trójkąt ABC na dwa trójkąty. Uzasadnij, że:
a) jest równoramienny
b) jeden z otrzymanych trójkątów jest podobny do trójkąta ABC.
|∡AEC| = 180deg−2x
|∡BEC| = 180deg − (180deg−2x)=2x
a) Ja zrobilbym to tak, ale nie wiem czy moje wnioski i sformulowania wpasowuja sie w klucz, w
dodatku wydaje mi sie, ze uzywam malo matematycznego jezyka.
|∡EAC| = |∡ECA| = x
|∡AEC| = 2x
⇒ trójkąt równoramienny, przy jednym boku występują kąty o tej samej mierze.
b) |∡ABC| = β,
w ΔABC mamy kąty: x, 2x, β
w ΔEBC mamy kąty: x, 2x, β (wspólny)
trójkąty podobne, cecha kąt−kąt−kąt