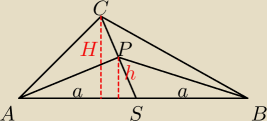
Dowod planimetryczny silnia: Punkt P nalezy do srodkowej CS trojkata ABC. Uzasadnij ze pola APC i BPC sa rowne. Moj sposob rozumowania: h_ΔAPS=h_ΔBPS=h

	ah
PΔAPS=
	2

	ah
PΔBPS=
	2

P_ΔAPS=P_ΔBPS h_ΔACS=h_ΔBCS=H

	aH
PΔACS=
	2

	aH
PΔBCS=
	2

P_ΔACS=P_ΔBCS

	aH		ah
PΔAPC=PΔACS−PΔAPS=		−
	2		2

	aH		ah
PΔBPC=PΔBCS−PΔBPS=		−
	2		2

P_ΔAPC=P_ΔBPC c.k.d

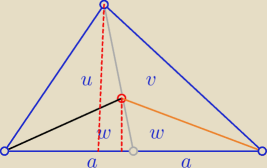Eta: w+u=w+v ⇒ u=v