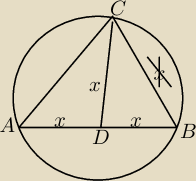
planimetria silnia: W trójkącie ABC z wierzchołka C poprowadzono środkową, która przecięła bok AB w punkcie D. Wiadomo, że |AD|=|BD|=|CD|. Wykaż, że jest to trójkąt prostokątny. Czy taki sposób poprzez opisanie okręgu na tym trójkącie, i wskazanie, że AD = DB = CD to promień okręgu, a AB jest przeciwprostokątną jest poprawne? Czy lepiej zrobić to w jakiś inny sposób?

ite: Pokazanie, że na tym trójkącie można opisać okrąg, którego średnicą będzie bok AB, jest bardzo dobry. Ładny zapis przeprowadzonego wnioskowania i masz max punktów za to zadanie : )

silnia: Jakies wskazowki?

ite: Proponuję kolejność: − na tym trójkącie można opisać okrąg o środku w D // wyjaśniasz dlaczego − bok AB jest jego średnicą // dlaczego akurat ten − na średnicy oparty jest trójkąt prostokątny − wniosek: ΔABC jest prostokątny

silnia: Opisuje okrag w srodku D, poniewaz do kazdego z wierzcholkow jest identyczna odlegosc (d), dalej nie wiem

Mila: Rachunek kątów i błyskawiczne uzasadnienie.

Mila: Do sposobu ite, zacząłeś dobrze, dalej : Kąt wpisany w okrąg oparty na średnicy jest prosty. 16:10 Podałam inny sposób . Spróbuj.

Mariusz: Zastosujmy twierdzenie cosinusów do trójkątów ADC i CDB (bo tam mamy kąty przyległe) Z twierdzenia cosinusów w trójkącie ADC b² = x²+x²−2*x*x*cos(δ) b² = 2x²−2x²cos(δ) Z twierdzenia cosinusów w trójkącie CDB a² = x²+x²−2*x*x*cos(180−δ) a² = x²+x²+2x*x*cos(δ) a² = 2x²+2x²cos(δ) Mamy zatem a² = 2x²+2x²cos(δ) b² = 2x²−2x²cos(δ) Dodajmy te równania stronami a²+b² = 4x² a²+b² = (2x)² Zatem z twierdzenia odwrotnego do twierdzenia Pitagorasa wnosimy że trójkąt ABC jest prostokątny