Potrzebuję pomocy przy rozwiązywaniu tego zadania
Maciek04: Punkty A(−6,2), B(2,−6) należą do prostej, która jest podstawą trójkąta ABC. Punkt C(−2,2) jest
wierzchołkiem trójkąta.
a)Oblicz odległość punkty C od prostej AB
b)Oblicz pole trójkąta ABC
29 mar 01:23
Jolanta: równanie prostej przechodzacej przez A i B
y=ax+b
|2=−6a+b \*(−1)
|−6=2a+b albo wzór na a
| | y2−y1 | | −6−2 | |
|−2=6a−b a= |
| = |
| =−1 |
| | x2−x1 | | 2−(−6) | |
|−6=2a+b
−8=8a
−1=a
2=−6(−1)+b
−4=b a=−1 b=−4 y=−x−4
postac ogólna prostej Ax+By+C=0
x+y+4=0 A=1 B=1 C=4
wzór na odległośc punktu P(x
0,y
0) od prostej Ax+By+C=0
29 mar 11:04
Jolanta: wysokośc trojkata h=d C(−2,2) x
0=−2 y
0=2
| | |1*(−2)+1*2+4| | | 4 | |
d= |
| = |
| =2√2 |
| | √12+12 | | √2 | |
h=2
√2
|AB|=
√(xB−xA)2+(yB−ya)2}=
√(2+6)2+(−6−2)2=
√64+64=
√2*64=8
√2
29 mar 11:17
Eta:
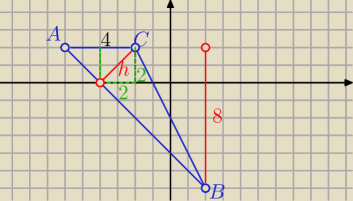
b) d= h= 2
√2
29 mar 12:36
