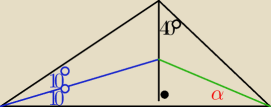
oblicz kąt Anna: oblicz kąt α nie wiem jak? i czy? wykorzystać dwusieczność niebieskiej

chichi: czy możesz wstawić oryginalne zdjęcie zadania?

Anna: nie mam... tylko tyle mi powiedzieli i twierdzą, że to na pewno wszystko co było..

ite: Czyli to punkt przecięcia dwusiecznej (niebieskiej) z wysokością trójkąta wyznacza drugie ramię kąta α?

Anna: tak

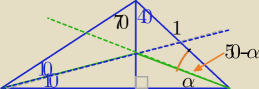
Mila: Tw.Cevy− wersja trygonometryczna

sin10o		sinα		sin40o
	*		*		=1⇔
sin10o		sin(50o−α)		sin70o

sin40o		sin(50o−α)
	=		, α∊(0,50o)
sin70o		sinα

2sin20o*cos20o		sin(50o−α)		2sin20o*		sin(50o−α)
	=		⇔		=
cos20o		sinα		1		sinα

sin20o		sin(50o−α)
	=
1   2		sinα

sin20o		sin(50o−α)
	=
sin30o		sinα

α=30^o ===

Qulka: dzięki dzięki dzięki

chichi: jutro wrzucę syntetyczne rozwiązanie, miłej nocy

Poli: Dziękuję, uwielbiam takie zadania, rozwiązywanie ich jest bardzo interesujące.

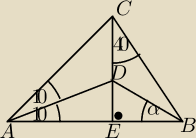
Mariusz: Można skorzystać ze szkolnej definicji tangensa kąta ostrego

	1
oraz tego że tg(90° − α) =
	tg(α)

Niech CE = h CD = y AE = x oraz AB = c AC = b BC = a Z ΔDEB otrzymujemy

	h−y
tg(α)=
	c−x

Z ΔAED otrzymujemy

	h−y
tg(10°) =
	x

Z ΔAEC otrzymujemy

	h
tg(20°) =
	x

Z ΔCEB otrzymujemy

	c−x
tg(40°) =
	h

Zatem

	h−y
tg(α)=
	c−x

	h−y		x
tg(α)=		*
	x		c−x

	h−y		h		x
tg(α)=		*		*
	x		c−x		h

tg(α)=tg(10°)tg(90°−40°)*tg(90°−20°) tg(α)=tg(10°)tg(50°)tg(70°) tg(α)=tg(10°)*tg(60°−10°)tg(60°+10°)

	√3−tg(10°)	√3+tg(10°)
tg(α)=tg(10°)
	1+√3tg(10°)	1−√3tg(10°)

	3−tg2(10°)
tg(α)=tg(10°)
	1−3tg2(10°)

	3tg(10°)−tg3(10°)
tg(α) =
	1−3tg2(10°)

	3−tg2(10°)   tg(10°)   1−tg2(10°)
tg(α) =
	1−3tg2(10°)   1−tg2(10°)

	2+1−tg2(10°)   tg(10°)( )   1−tg2(10°)
tg(α) =
	1−tg2(10°)−2tg2(10°)   1−tg2(10°)

	2   tg(10°)( + 1)   1−tg2(10°)
tg(α) =
	2tg2(10°)   1−   1−tg2(10°)

	2tg(10°)   +tg(10°) 1−tg2(10°)
tg(α) =
	2tg(10°)   1− *tg(10°)   1−tg2(10°)

tg(α) = tg(20°+10°) tg(α) = tg(30°) α = 30°

Mariusz: Jak widać rozwiązanie krótkie nie zawsze jest piękne Moje rozwiązanie ma tę przewagę nad rozwiązaniem Mili że nie korzystam z dziwnych twierdzeń których nie ma w programie nauczania liceum Korzystam ze szkolnej definicji tangensa kąta ostrego (Za czasów gdy podstawówka była ośmioklasowa to było nawet w podstawówce) tg(α)tg(90° − α) = 1 (To też było w ośmioklasowej podstawówce)

	tg(α)+tg(β)
tg(α+β)=
	1−tg(α)tg(β)

(Na pewno ten wzorek był w liceum . Czy był w podstawówce tego nie jestem pewien ale chyba nie)