Układ równań z dwoma równaniami okręgu
Althea:
Dzień dobry!
Przede mną zadanie o takiej treści:
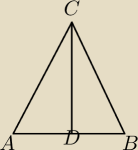
W trójkącie równoramiennym ABC o ramionach AC i BC dane są A = (−3,−4) i B = (5,2). Wysokość
trójkąta poprowadzona do podstawy AB ma długość 10. Wyznacz współrzędne punktu C.
Wszystko pięknie − oznaczyłam współrzędne punktu C jako (x,y) obliczyłam długość podstawy (10),
współrzędne punktu D (1,−1), boków AC i BC (5
√5) z tw. Pitagorasa.
Zapisałam odcinki AC i BC wzorem na długość odcinka ze współrzędnych punktów:
|AC| =
√(x+3)2+(y+4)2 =
√125
|BC| =
√(x−5)2+(y−2)2 =
√125
I podniosłam do kwadratu:
(x+3)
2+(y+4)
2 = 125
(x−5)
2+(y−2)
2 = 125
A tu zonk − układ równań z dwoma okręgami. Rozumiem, że ich punkt przecięcia to będą dwie
możliwości punktu C (jedna wyjdzie (−5,7), druga (7,−9), jak patrzyłam na Geogebrę), ale jak
go rozwiązać to nie mam pojęcia.
Próbowałam też z odległością punktu od prostej, prosta przechodząca przez A i B mi wyszła
y=3/4x+5/4, ale z tego mi wynikło tylko równanie |3x+4y+5|=50. Niby by można próbować dłubać z
jednym okręgiem i tą odległością, ale moduły nigdy nie były moją mocną stroną...
 Dzień dobry!
Przede mną zadanie o takiej treści:
W trójkącie równoramiennym ABC o ramionach AC i BC dane są A = (−3,−4) i B = (5,2). Wysokość
trójkąta poprowadzona do podstawy AB ma długość 10. Wyznacz współrzędne punktu C.
Wszystko pięknie − oznaczyłam współrzędne punktu C jako (x,y) obliczyłam długość podstawy (10),
współrzędne punktu D (1,−1), boków AC i BC (5√5) z tw. Pitagorasa.
Zapisałam odcinki AC i BC wzorem na długość odcinka ze współrzędnych punktów:
|AC| = √(x+3)2+(y+4)2 = √125
|BC| = √(x−5)2+(y−2)2 = √125
I podniosłam do kwadratu:
(x+3)2+(y+4)2 = 125
(x−5)2+(y−2)2 = 125
A tu zonk − układ równań z dwoma okręgami. Rozumiem, że ich punkt przecięcia to będą dwie
możliwości punktu C (jedna wyjdzie (−5,7), druga (7,−9), jak patrzyłam na Geogebrę), ale jak
go rozwiązać to nie mam pojęcia.
Próbowałam też z odległością punktu od prostej, prosta przechodząca przez A i B mi wyszła
y=3/4x+5/4, ale z tego mi wynikło tylko równanie |3x+4y+5|=50. Niby by można próbować dłubać z
jednym okręgiem i tą odległością, ale moduły nigdy nie były moją mocną stroną...
Dzień dobry!
Przede mną zadanie o takiej treści:
W trójkącie równoramiennym ABC o ramionach AC i BC dane są A = (−3,−4) i B = (5,2). Wysokość
trójkąta poprowadzona do podstawy AB ma długość 10. Wyznacz współrzędne punktu C.
Wszystko pięknie − oznaczyłam współrzędne punktu C jako (x,y) obliczyłam długość podstawy (10),
współrzędne punktu D (1,−1), boków AC i BC (5√5) z tw. Pitagorasa.
Zapisałam odcinki AC i BC wzorem na długość odcinka ze współrzędnych punktów:
|AC| = √(x+3)2+(y+4)2 = √125
|BC| = √(x−5)2+(y−2)2 = √125
I podniosłam do kwadratu:
(x+3)2+(y+4)2 = 125
(x−5)2+(y−2)2 = 125
A tu zonk − układ równań z dwoma okręgami. Rozumiem, że ich punkt przecięcia to będą dwie
możliwości punktu C (jedna wyjdzie (−5,7), druga (7,−9), jak patrzyłam na Geogebrę), ale jak
go rozwiązać to nie mam pojęcia.
Próbowałam też z odległością punktu od prostej, prosta przechodząca przez A i B mi wyszła
y=3/4x+5/4, ale z tego mi wynikło tylko równanie |3x+4y+5|=50. Niby by można próbować dłubać z
jednym okręgiem i tą odległością, ale moduły nigdy nie były moją mocną stroną...