Podzielnosc 5" - 2" przez 9
tomeczek2: Dla ktorych z podanych liczb n liczba 5" − 2" jest podzielna przez 9?
n = 60
n = 33
n = 20
n = 45
Probowalem cos dzialac wzorami skroconego mnozenia ale nic na razie nie wyszlo

26 mar 19:24
chichi:
co oznacza zapis 5
'' 
26 mar 19:32
tomeczek2: Kurcze, nie zauwazylem, ze sie tak dziwnie skopiowalo. Mialo tam byc po prostu "n".
26 mar 19:49
wredulus_pospolitus:
5a − 2a = (5−2)*(5a−1 + 5a−221 + ... + 5a−k*2k−1 + .... + 51*2a−2 + 2a−1)
26 mar 20:04
wredulus_pospolitus:
tak więc −−− pytanie brzmi kiedy drugi nawias będzie podzielny przez 3
26 mar 20:05
ABC:
Jak ci nie wyszło wzorami skróconego mnożenia jeśli 53−23=125−8 =117 ,a to się dzieli przez 9
?
zatem dla 60,33,45 odpowiedź pozytywna bo są postaci 3p dla pewnego p
a dla 20 sam udowodnij że się nie podzieli
26 mar 20:06
tomeczek2: nadal nie wiem jak to zrobic
2 kwi 00:58
ABC:
cienki jesteś jak drut wolframowy w dawnych żarówkach
560−260=(53)20−(23)20= (wzór wredulusa) = (53−23) (coś) =117*coś =9*13*coś
i analogicznie pozostałe które dzielą się przez 3
2 kwi 09:21
tomeczek2: pocisk z rigczem, za to dla 20 nadal nie wiem jak uzasadnic ze sie nie da niestety
2 kwi 20:56
ABC:
zmień pracę ,weź kredyt , nie musisz się zajmować matematyką
2 kwi 21:24
tomeczek2: no niestety poki chodze do szkoly to musze:(
2 kwi 21:58
ABC: takich zadań jak wyżej nie ma na podstawie , zmień rozszerzenie na angielski i spokój masz

2 kwi 22:30
tomeczek2: angielski juz rozszerzam lol
2 kwi 22:39
tomeczek2: ale nadal wolalabym sie mimo wszystko dowiedziec jak to rozwiazac
2 kwi 22:39
tomeczek2: moglby mi ktos pomoc z tym zadaniem prosze
3 kwi 20:25
ABC:
Nie pokazałeś leniu nic wkładu własnego , żadnego prób, ja ci więcej nie pomogę
3 kwi 20:45
tomeczek2: chodzi o to że jedyny sposób jaki znam na udowodnienie to zrobienie z czegoś 9k +
(1,2,3,4,5,6,7,8) a nie mam pojęcia jak z tej różnicy zrobić sumę takiej właśnie postaci
3 kwi 21:12
k: Sprawdź jakie reszty z dzielenia przez 9 dają kolejne potęgi liczb 5 i 2.
Zauważysz, że się zapętlają.
3 kwi 21:23
tomeczek2: sprawdzilem roznice od 51 − 21 do 55 − 25 i zauwazam ze dla potegi 3 reszta jest rowna 0 a
dla pozostalych jest rowna 3 zatem nie sa one podzielne tylko teraz jak to zapisac dowodowo
3 kwi 21:33
k: sprawdź potęgi liczb 5 i 2 a nie ich różnice.
Zauważysz, że 52 daje taką samą resztę z dzielenia przez 9 jak 58 , 514 i 520 i jest to
7
Analogicznie jest dla 22 , 28 , 214 , 220 z resztą 4.
Czyli
520 − 220 daje z dzielenia przez 9 resztę 7 − 4 = 3.
Podzielne, więc nie jest.
3 kwi 21:51
tomeczek2: Jak mam sprawdzić resztę z dzielenia takiej dużej liczby jak np. 514?
3 kwi 22:03
Mila:
520−220=(55)4−(25)4=((55)2−(25)2)*((55)2+25)2)=
=(55−25)*(55+25)*[(55)2+25)2]=
=(55−25)*(55+25)*[(510+(210]
dalej:
1) (55−25)= licz z wzoru albo kalkulator to jest podzielne przez 3
2) (55+25) wystarczy nam podzielność przez 3
52=3k+1
55=52*52*5=(3k+1 )*(3k+1)*(3+2)= 3p+2 , p∊N ( mnożysz reszty )
25=32 =3*10+2
55+25=3p+2+3*10+2=3(p+10) +4=3(p+10)+3+1 reszta 1
liczba (55+25) nie jest podzielna przez 3
3) 510=(52)5=(3k+1)5 =3*(m)+1 reszta 1
210=(25)2=(3a+2)*(3a+2)=..
dokończysz teraz?
3 kwi 22:08
tomeczek2:
= 3b + 4 reszta 4
510 + 210 = 3m + 1 + 3b + 4 = 3n + 2 nie jest podzielne przez 3
cały iloczyn = [3x] * [(3y + 1) * (3z + 2)] = (podzielne przez 3(ale nie 9)) *
(niepodzielne przez 3) = niepodzielne przez 3
dobrze to robie? o to chodzi?
3 kwi 22:22
tomeczek2: *na końcu chodziło mi o niepodzielne przez 9 a nie 3
3 kwi 22:41
Mila:
Reszta z dzielenia przez 3 jest mniejsza od 3 . (0,1,2}
Może być, ale zapis pierwszej linijki:
3b+1=3b+4=3b+3+1=3(b+1)+1 reszta 1
dalej dobrze.

3 kwi 23:01
tomeczek2: rozumiem dziekuje slicznie za pomoc
3 kwi 23:18
Mila:

3 kwi 23:21
an: dla n=3k
(3+2)3k−23k=(33+3*32+3*3*22+23)k−23k=9(33k−2.......)+23k −23k
jak widać dla n podzielnego przez 3 wyrażenie jest podzielne przez 9
3 kwi 23:44
an: tomeczku2 a wiesz już co z pozostałymi n
4 kwi 11:11
circle:
Ad 22:22
zamiast [3x] powinieneś zapisać 3*1031, aby pokazać,
że 55−25 dzieli się przez 3 i nie dzieli się przez 9.
4 kwi 14:47
dr Wolf (katedra algebry mat.): czy znasz cechę podzielności przez 9?
dr. Anatol Wolf, katedra całek i algebry matematycznej uniwersytetu
4 kwi 16:32
an:
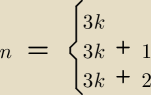
5
3k+1−2
3k+1=(3+2)
3k+1−2
3k+1=5*(33+3*32+3*3*22+2
3)
k−2*2
3k=
=5*9*(3
3k−2.......)+2*2
3k −2
3k=5*9*(3
3k−2+.......)+2
3k niepodzielne przez 9
(3+2)
3k+2−2
3k+2=25*9*(3
3k−2+.......)+25*2
3k −2
3k=
=25*9*(3
3k−2+.......)+24*2
3k niepodzielne przez 9
4 kwi 18:17
tomeczek2: dziekuje za Wasze odpowiedzi, Mila mi juz wytlumaczyła

4 kwi 19:44
mydlix: 5n−2n=3*(5n−1+5n−22+5n−322+...+522n−3+5*2n−2+2n−1) z tożsamości
nieśmiertelnej.
Jeśli 9 ma dzielić 5n−2n, to oczywiście drugi nawias musi być podzielny przez 3. Jako, że 5≡2
(mod 3), to
5n−1+5n−22+5n−322+...+522n−3+5*2n−2+2n−1 ≡ n5n−1 (mod 3), czyli n musi
być podzielne przez 3
Można też skorzystać z LTE (lub LZW), jeśli ktoś zna: jako że 3 dzieli 5−2 oraz 3 nie dzieli
5*2, to można napisać:
2≤v3(5n−2n)=v3(5−2)+v3(n)=1+v3(n)
skąd v3(n)≥1, czyli 3 musi dzielić n
Z obu sposobów wynika, że 9 dzieli 5n−2n wtedy i tylko wtedy, gdy 3 dzieli n.
4 kwi 20:59
mydlix: Trudniejsze zadanie: wykazać, że jeśli n dzieli 5n−2n, to 3 dzieli n
4 kwi 21:02





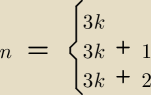 53k+1−23k+1=(3+2)3k+1−23k+1=5*(33+3*32+3*3*22+23)k−2*23k=
=5*9*(33k−2.......)+2*23k −23k=5*9*(33k−2+.......)+23k niepodzielne przez 9
(3+2)3k+2−23k+2=25*9*(33k−2+.......)+25*23k −23k=
=25*9*(33k−2+.......)+24*23k niepodzielne przez 9
53k+1−23k+1=(3+2)3k+1−23k+1=5*(33+3*32+3*3*22+23)k−2*23k=
=5*9*(33k−2.......)+2*23k −23k=5*9*(33k−2+.......)+23k niepodzielne przez 9
(3+2)3k+2−23k+2=25*9*(33k−2+.......)+25*23k −23k=
=25*9*(33k−2+.......)+24*23k niepodzielne przez 9
