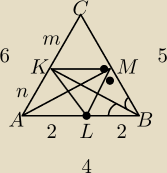
trójkąt chair: Dany jest ΔABC: AB=4, BC=5 i AC=6. Punkt L = śr.AB. M = spodek wysokości opuszczonej z wierzchołka A. K = punkt przecięcia dwusiecznej kąta B z bokiem AC. Oblicz pole i obwód ΔKLM

	10		8
1) Z twierdzenia o dwusiecznej wyznaczyłem m=		i n=
	3		3

	15√7		ah
2) Potem (obliczając pole ΔABC ze wzoru herona (		) i przyrównując do		)
	4		2

	3√7
wyznaczyłem wysokość (AM) h=
	2

	1		9
3) Znając h w ΔABM z Tw. Pitagorasa wyznaczyłem BM=		, czyli CM=
	2		2

4) Teraz biorę się za wyliczenie boków ΔKLM: a) Łatwo zauważyć, że LM=2 (LM = r okręgu opisanego na Δprostokątnym)

	MC		4,5		3
b) Z ΔAMC wyznaczyłem cos γ =		=		=		i od razu z Tw. Carnota w ΔCKM
	AC		6		4

	√319
wyliczam KM =
	6

	cbsinα
c) Ze wzoru na pole ΔABC		i przyrównując do wcześniej wyliczonego pola ze wzoru
	2

	15√7		5√7		9
herona (		) wyznaczam sin α =		i ze wzoru jedynkowego cos α = +−
	4		16		16

	√154
potem z Tw. Carnota w ΔALK (uwzględniając kąt dodatni i ujemny) wychodzi KL=		lub
	3

	√46
		.... i co teraz ? sprawdziłem czy oba będą spełniać nierówność ΔKLM i spełniają
	3

więc jaki wynik odrzucić ? bo żeby wyliczyć pole ΔKLM to wystarczy od pola ΔABC odjąc te 3 pozostałe pola (które się łatwo wyliczy ze wzoru z sinuem kąta między dwoma bokami) ale do wyliczenia obwodu tego ΔKLM jednak jakiś wynik odcinka KL trzeba odrzucić, co teraz? Wszystko zaczęło się od wzoru jedynkowego, który mi "wypluł" 2 wyniki cosα i w zasadzie żadnego z góry nie moge odrzucić bo może być to kat ostry jak i rozwarty (cos γ i cos β są dodatnie)

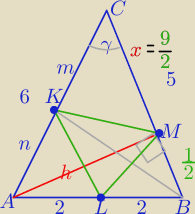Mila: 1)ΔABC jest Δ ostrokątnym.

	1
∡B jest największym kątem i cosβ=		>0
	8

cosA>0 z tw. cosinusów 2) Za bardzo skomplikowałeś obliczenia.

Kastet: Okej faktycznie czyli cosA będzie tez dodatni Natomiast to był moj jedyny pomysł by dotrzeć do pola ΔKLM i jego obwodu. Wyliczyłem to co mogłem wyliczyć

a7: to może obliczyć wszytskie cosinusy i sinusy (z twierdzenia cosinusów) i potem od ΔABC odjąć Pola ALK MBL i KMC

Mila: Tak liczył chair, ale to żmudne rachunki. Ciekawa jestem, czy ma odpowiedź.

an: pole ze stosunków pól do całości ΔKLM/ΔABC= 1−1/2−2/9−1/20=41/180

	41√7
ΔKLM=
	48

boki policzone prawidłowo, ale ich suma chyba za ładna nie będzie

Mila: Też liczyłam ze stosunków pól. Wynik mam taki sam jak we wpisie 20:32.

.: W jaki sposób ze stosunków?

123: Czy to jest po prostu odjęcie pól ALK MBL KMC od ABC?

Mila:

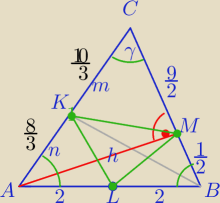
	15√7
PΔABC=		=P jak obliczył chair, a także pozostałe wartości na rysunku.
	4

1) (zapis [AMC] oznacza pole ΔAMC)

[AMC]		9		9		1
	=		⇔ [AMC]=		P i [ABM]=		P
[ABM		1		10		10

[CKM]		10		5
	=		=		⇔4[CKM]=5[AKM]
[AKM		8		4

	4		9
[CKM]+		[CKM]=		P⇔
	5		10

	1
[CKM]=		P
	2

=========== 2) [ALM]=[LBM]⇔

	1
[LBM]=		P
	20

======== 3)

[BKC]		10		5
	=		=		⇔
[BKA]		8		4

	4
[BKA]=		P ale [ALK]=[LBK]⇒
	9

	2
[ALK]=		P
	9

======== 4)

	1		1		2
[KLM]=P−(		P+		P+		P)=
	2		20		9

	90+9+40		139		41
=P−		P=P*(1−		)=		P
	180		180		180

5)

	15*41√7
[KLM]=
	180*4

	41√7
PΔKLM=
	48

=========== ===========

123: a spoko przez chwilę o tym pomyślałem, dzięki Aczkolwiek z tw cosinusów i wz. Herona żmudnie... ale pewnie podobnie czasowo, może nie rachunkowo, ale jednak trzeba by obwód więc do tego byłaby ta droga rozsądniejsza.

Mila: Pisałam dokładne rachunki, ale pewne zależności ustalałam w pamięci i było krócej. Niewiele oszczędności czasowej, ale bez pierwiastków. Obwodu nie liczyłam, warto się zastanowić, czy coś się zyska bez tw. cosinusów. Liczyłeś? |LM|=2

	√319
|KM| =		z tw. Stewarta niewiele mniej rachunków
	6

|KL|=tw. cosinusów, cosinus ładny

	9
cosA=
	16

	√46
|KL|=
	3

	√319		√46
2p=2+		+
	6		3

	1
Pole trójkąta ABC obliczyłam z wzoru :		*|BC|*h − bez Herona, ale można bo,
	2

boki wyrażone liczbami całkowitymi.

Mila: Skrócone obliczenia, bez pośrednich objaśnień. P_ΔABC=P − obliczone wyżej oraz długości odcinków na rys. 16:04 1)

	[ABM]		(1/2)		1
		=		=
	P		5		10

	1		1
[ABM]=		P to [LBM]=		P
	10		20

2)

[AKB]		(8/3)		4
	=		=
P		6		9

	2		2
[AKB]=		P to [ALK]=		P
	9		9

3)

[CKM]		(10/3)*(9/2)*sinγ		1
	=		=		⇔
P		6*5*sinγ		2

	1
[CKM]=		P
	2

dalej j.w.