Funkcja kwadratowa z parametrem Szambonur: Wyznacz wszystkie wartości parametru m, m ∊ R dla których równanie x 2 − (2m − 3) * x + m − 1 = 0 ma dwa różne rozwiązania rzeczywiste takie, że każde z nich jest większe od 1. Zapisz obliczenia. Nie mogę dojść do tego jak obliczyć by obydwa x były większe od 1. Próbowałem skorzystać ze wzorów viete'a: Skoro obydwa x mają być większe od 1 to dodane do siebie będą większe niż 2, a pomnożone większe od jeden, ale jak to podstawiam i tworzę układ równań to wynik, który mi wychodzi ni jak się nie klei z odpowiedzią do zadania. Dziękuję za pomoc

chichi: jeśli zdefiniujemy funkcje f: R → R daną wzorem f(x) = x² − (2m − 3)x + m − 1, to wiemy na pewno, że jej wykresem jest parabola o ramionach skierowanych w górę, wyrzuć wierzchołek za jedynkę czyli p > 1, no ale wciąż lewa gałąź paraboli może przecinać oś OX przed 1, aby tego uniknąć narzuć warunek, aby ją wypchnąć nad, czyli f(1) > 0, te 2 warunki powinny doprowadzić Cię do prawidłowej odp.

Tadeusz: ... a o Δ i tak nie zapominaj

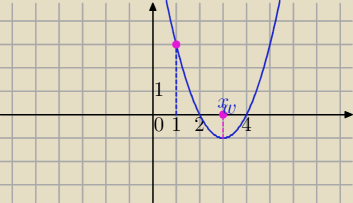
Mila: Δ>0 i f(1)>0 i x_w>1

Mila: O, przepraszam, chichi już podał (p>1).