planimetria Fabian: dany jest trojkat rownoramienny ABC o podstawie AB dlugosci 12 i ramionach dlugosci 24. Oblicz dlugosc odcinka dwusiecznej z wierzcholka A zawartego w tym trojkacie

Mariusz: Dla trójkąta dowolnego o danych długościach boków Z twierdzenia sinusów w ΔADC

x		b
	=
sin(α)		sin(δ)

x		sin(α)
	=
b		sin(δ)

Z twierdzenia sinusów w ΔADB

a−x		c
	=
sin(α)		sin(180−δ)

a−x		c
	=
sin(α)		sin(δ)

a−x		sin(α)
	=
c		sin(δ)

zatem porównując obydwa wyniki mamy

x		a−x
	=
b		c

Z twierdzenia cosinusów w ΔABC c²=a²+b²−2abcos(γ) Z twierdzenia cosinusów w ΔADC d²=b²+x²−2bxcos(γ)

x		a−x
	=
b		c

cx = b(a−x) cx = ab − bx cx+bx = ab x(b+c) = ab

	ab
x =
	b+c

c²=a²+b²−2abcos(γ) 2abcos(γ) = a²+b²−c²

	a2+b2−c2
cos(γ) =
	2ab

d²=b²+x²−2bxcos(γ)

	a2b2		2ab2	a2+b2−c2
d2 = b2+		−
	(b+c)2		(b+c)	2ab

	a2b2		b(a2+b2−c2)
d2 = b2+		−
	(b+c)2		b+c

	b2(b+c)2+a2b2−b(b+c)(a2+b2−c2)
d2 =
	(b+c)2

	bc(b2+2bc+c2−a2)
d2 =
	(b+c)2

	bc((b+c)2−a2)
d2 =
	(b+c)2

	bc(b+c − a)(b+c+a)
d2 =
	(b+c)2

chichi:

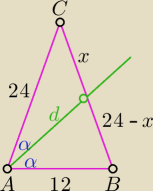
	x		24
(1) tw. o dwusiecznej:		=		⇔ x = 16
	24 − x		12

(2) tw. Stewarta: 12² * 16 + 24² * 8 = 24(d² + 16 * 8) ⇔ d = 4√10

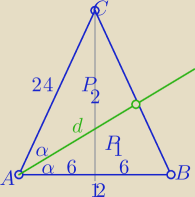
Eta: Inny sposób (bez Stewarta i "kosmicznych" wzorów Z porównania pól:

	6		1
PABC= 36√15 i cos(2α)=		=
	24		4

P_ABC=P₁+P₂

1		1
	*12*d*sinα+		*24*d*sinα= 36√15
2		2

	2√15
d=
	sinα

	√3
cos(2α)=1−2sin2α ⇒ sinα=
	2√2

	2√2
d= 2*√3*√5*
	√3

d=4√10 =========

Mariusz: Jakich kosmicznych wzorów ? Twierdzenie sinusów i cosinusów było w podstawie programowej jakieś ćwierć wieku temu i zdaje się że nadal jest w programie a co do sposobu z polami to zdaje się że kiedyś go pokazywałaś i to chyba nawet dla trójkąta dowolnego

chichi: tw. Stewarta jest następstwem tw. Carnota, więc jest równie banalne

Mariusz: chichi czyli twoje rozwiązanie jest zbliżone do mojego tyle że licealiści prawdopodobnie twierdzenia Stewarta nie mają więc jeżeli chcesz z niego korzystać to wypadałoby je podać wraz z dowodem Ja z dwukrotnego zastosowania twierdzenia sinusów wyprowadziłem tzw twierdzenie o dwusiecznej a następnie z dwukrotnego zastosowania twierdzenia cosinusów obliczyłem długość odcinka dwusiecznej Rozwiązanie Ety jest całkiem niezłe ale czy ominiemy w ten sposób twierdzenie cosinusów ? Do obliczenia pola trójkąta ABC potrzebujemy wartość sinusa Tutaj mamy trójkąt równoramienny więc dałoby radę ale w trójkącie dowolnym ...

chichi: rozwiązujący nigdy nie musi podawać dowodów twierdzeń z których korzysta, jeśli stosuje je poprawnie. Osoba sprawdzająca powinna być na tyle kompetentna, aby sama mogła sprawdzić poprawność owego rozwiązania i zastosowania twierdzenia, nawet jeśli go nie zna

Mariusz: Nie znasz się na nauczaniu i na tym co jest i było w szkole Ba nawet na studiach jeżeli nie rozwiążesz zadania sposobem oczekiwanym przez prowadzącego to może ci tego rozwiązania nie uznać Nie ma w programie więc z prawdopodobieństwem bliskim jedności można stwierdzić że takiego rozwiązania nie uznają więc twoje rozwiązanie można wyrzucić do śmieci

chichi: bo w Polsce uczą ograniczeni umysłowo ludzie i zabijają ambicje uczniów, którzy potrafią być bardziej sprytni od nich samych. każą im rozwiązywać równania typu x² − 4 = 0 przez deltę, bo tak było na lekcji. Przestarzały system edukacji, który zabija piękno matematyki, ale Ty matematykiem nie jesteś, ani nie aspirujesz, wiec nie zrozumiesz. koło Ameryki to to nawet nie leżało

Mariusz: Fabian jeżeli nie chcesz dostać niedostatecznej to sprawdź czy w programie liceum jest twierdzenie sinusów i cosinusów Jeżeli jest to możesz wybrać zarówno moje rozwiązanie jak i rozwiązanie Ety Jeżeli nie ma twierdzenia sinusów i cosinusów w programie to wybierz rozwiązanie Ety Na pewno za "rozwiązanie" chichiego zostaniesz nagrodzony niedostateczną no najwyżej mierną (bo zastosował twierdzenie o dwusiecznej które to wam ostatnio wprowadzili) Za moich czasów nie było twierdzenia o dwusiecznej w programie a przynajmniej ja go sobie nie przypominam Było za to twierdzenie sinusów na podstawie programowej (wtedy chyba się podstawa nazywała minimum programowym)

Mariusz: A ty nigdy nie będziesz nauczycielem

chichi: ba, nawet nie chcę. nie studiuję nauczania matematyki tylko matematykę teoretyczną

Mila: Mariusz nie masz racji. Twierdzenie o dwusiecznej zawsze było w programie LO, a także GM. Nie pamiętam, czy było w VIII klasie przed wprowadzeniem GM. Tw. Stewarta podaje się na kółkach matematycznych. ( zamiast np. dwa razy korzystać z tw. cosinusów można szybko obliczyć dł. ceviany stosując tw. Stewarta)

Fabian: o matko bosko co tu sie stanelo

Mila: Dyskusja Tak tu czasem bywa.

an: Szanowni pedagodzy

	sinα
Tu wystarczy znać wzór na pole trójkąta P=b*c		oraz cos2α
	2

sinα		sinα		sin2α
	*24d+		*12d=		*24*12
2		2		2

d=16cosα

	1		5
cos2α=		⇒cosα=√
	4		8

d=4√10