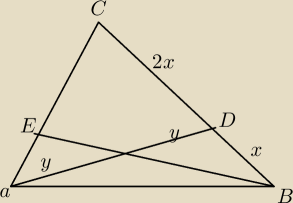
Planimetria PR silnia: W trójkącie ostrokątnym ABC punkt D dzieli bok BC w stosunku 1:2 licząc od wierzchołka B . Z wierzchołka B poprowadzono prostą przechodzącą przez środek odcinka AD , która przecięła bok AC w punkcie E . Oblicz, w jakiej proporcji, licząc od wierzchołka A , punkt E dzieli bok AC .

chichi: narysuj, pokaż swoje próby, bo Ty hurtowo walisz tutaj te zadania...

silnia:

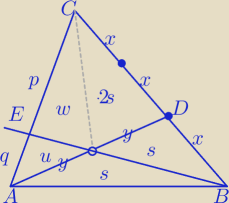
Mila: Małymi literami oznaczono pola Δ.

p		w		w+3s
	=		=
q		u		u+s

w*(s+u)=u*(w+3s) ws+wu=uw+3su ws=3su w=3u

p		3u		3
	=		=
q		u		1

silnia: Jakie to twierdzenie?

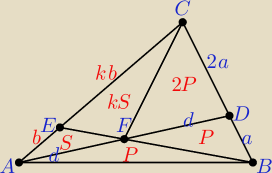
Niuton: P, S − pola trójkątów P_BCE = k*P_ABE ⇒ 3P + kS = kS + kP ⇒ k = 3

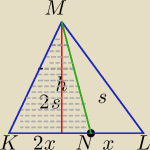
Mila: ad. 20: 23 ΔKNM i ΔNLM mają taką samą wysokość;

PKNM		12*2x*h		2x		2
	=		==		=
PΔNLM		12*x*h		x		1

P_ΔKNM =2*P _ΔNLM