Dany jest prawidłowy ostrosłup czworokątny ABCDS o podstawie ABCD uczen: Dany jest prawidłowy ostrosłup czworokątny ABCDS o podstawie ABCD. Na krawędzi CS zaznaczono punk E w ten sposób, że AB=2CE. Wiedząc, że płaszczyzna BDE jest prostopadła do krawędzi CS, wyznacz cosinus kąta BED. Mam problem z zaznaczeniem, w którym miejscu jest ten kąt prosty pomiędzy płaszczyzną , a krawędzią CS, ktoś pomoże?

ite:

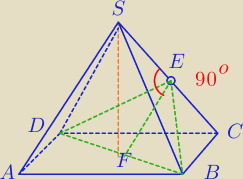
ite: Kąt 90^o tworzy prosta CS z każdym z odcinków EB, EF i DE (gdyż leżą w płaszczyźnie prostopadłej do tej prostej). Na rysunku zaznaczyłam tylko jeden z tych kątów, żeby nie zaciemniać obrazu.

uczen: Dobrze rozumiem ze kat BEC tez ma 90 stopni?

ite: tak

uczen: Czyli w takim razie odcinek BE=DE=√3/2x nastepnie z tw cos wyliczamy i wychodzi cosα=−1/3 dobrze rozumiem ?

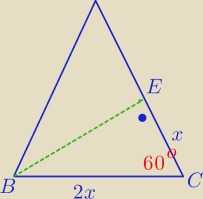
ite: ΔBEC jest szczególnym trójkątem prostokątnym, |BE| = √3*x, dalej można oczywiście skorzystać z twierdzenia cosinusów

ite:

	1
odp. się zgadza, cosα=−
	3

uczen: dzieki

james1: Hi friends how ae you all . I hope you all will be fine. I like this forum so much because I love math. It is one of my favorite subject<a href="http://techemirate.com/endoscope-camera-for-pc-windows-mac/>.</a>