| b | ||
fw(xw)=2 (xw=− | ) | |
| 2a |
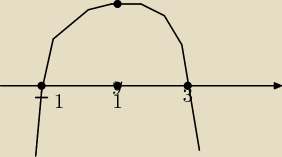 y=ax2+bx+c Do wzoru podstawiamy punkty: (−1,0), (3,0) i wierzchołek (1,2).
Rozwiązać należy układ równań:
0=a−b+c
0=9a+3b+c
2=a+b+c
y=ax2+bx+c Do wzoru podstawiamy punkty: (−1,0), (3,0) i wierzchołek (1,2).
Rozwiązać należy układ równań:
0=a−b+c
0=9a+3b+c
2=a+b+c
| 1 | 1 | |||
Stąd: a= − | , b = 1, c= 1 | . | ||
| 2 | 2 |
| 1 | 1 | |||
Czyli wzór funkcji jest: y = − | x2 + x + 1 | |||
| 2 | 2 |
| −Δ | ||
Rzędna wierzchołka yw= | więc | |
| 4a |
| 4a2+4a*3a | 1 | |||
− | =2 ; a=− | |||
| 4a | 2 |
| 1 | 3 | |||
F(x)=− | x2+x+ | |||
| 2 | 2 |