Trygonometria silnia: Równanie sin²x+sinx=2 a) nie ma rozwiązań rzeczywistych b) ma dokładnie jedno rozwiązanie rzeczywiste c) ma dokładnie dwa rozwiązania rzeczywiste d) ma nieskończenie wiele rozwiązań rzeczywistych Mi wydaje sie, ze prawidlowa jest odpowiedz c), jednak w kluczu mam d). Sposob rozwiazania: sin²x+sinx=2 sin²x = 1 ∧ sinx=1 (bo zbiór wartosci funkcji to <−1,1>, a dla kwadartu <0,1>) sinx=−1 ∨ sinx=1 ∧ sinx=1 x = pi/2 lub −pi/2

chichi: tam na dole trzeba by nawias wstawić, jak rozbijasz na alternatywę! jest ok, ale popatrz na to równanie, jak na równanie kwadratowe, którego zmienną jest sin(x) i dojdziesz do postaci (sin(x) + 2)(sin(x) − 1) = 0, w tym przypadku z prawej strony równania była krytyczna wartość, więc wnioskowanie było proste, natomiast gdy stałoby tam co innego, już byś tak postąpić nie mógł. Jeśli chcesz to w szkole uczą nawet metody podstawienia u = sin(x) i masz wówczas równanie u² + u = 2, rozwiązujesz względem u i wracasz do podstawienia

Eta: sin²x+sinx−2=0 (sinx+2)(sinx−1)=0 sinx=−2 −− sprzeczność lub sinx=1

	π
x=		+2kπ , k∊ℤ −−− niesk. wiele rozw. rzeczywistych
	2

Odp: d)

chichi:

	π
mamy rozw. x =		+ 2kπ, gdzie k ∊ ℤ − tych rozw. jest niesk. wiele, nie wiem skąd u
	2

	π		π		π
Ciebie wzięło się −		, przecież sin(−		)=−sin(		) − stąd już widać, że wartości
	2		2		2

w tych punktach są przeciwne, poprawna jest więc odp. D

silnia: No tak. Plus okresowosc rozwiazania, zapomnialem. W przedziale byloby np 2 rozwizania, dzieki.

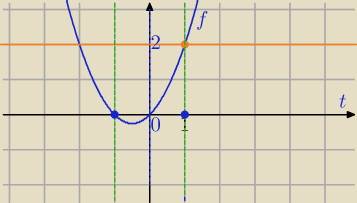
Mila: f(x)=sin²x+sinx−2 sin(x)=t, t∊<−1,1> f(t)=t²+t t²+t=2 Wartość f(t)=2 dla t=1

	π
sin(x)=1⇔x=		+2kπ , k∊C
	2

nieskończenie wiele rozwiązań.