W ostrosłupie prawidłowym trójkątnym o wysokości H HEJ: W ostrosłupie prawidłowym trójkątnym o wysokości H= 5√5 przekrój przechodzący przez wierzchołek tego ostrosłupa oraz środki dwóch sąsiednich krawędzi podstawy ma pole 24√2. Oblicz objętość tego ostrosłupa Pomocyyy

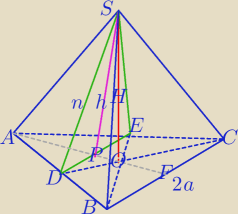Mila: |DE|=a 1)

	1
PΔDES=		|DE|*h=24√2
	2

a*h=48√2

	2		1		a√3
|AF|=a√3, |OP|=		a√3−		a√3=
	3		2		6

2)

	a√3
h2=(		)2+H2
	6

	a2
h2=		+125
	12

a²*h²=48²*2

	4608
h2=
	a2

4608		a2
	=		+125 /*a2
a2		12

	a4
4608=		+125 a2
	12

a4
	+125 a2−4608=0, a>0
12

	1
Δ=15625+4*		*4608
	12

√Δ=131

	−125−131		−125+131
a2=		<0 lub a2=		=36
	16		16

a=6 2a=12

	1		144√3
V=		*		*5√5
	3		4

V=60√15 ======

a7: Skąd wiadomo jak obiczyć OP?

a7: a już wiem, ok,

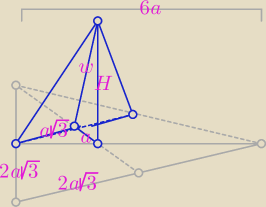bonus: W takich sytuacjach wybieram najkrótszy odcinek i oznaczam go jakąś literką, tutaj literką a. Szkic rozwiązania: Z treści zadania: a√3 w = 24√2 /² i (tw. Pitagorasa) 125 + a² = w² 3a² (125 + a²) = 24²*2 /:3 ⇒ a⁴ + 125a² − 384 = 0, Δ = 131², a² = 3 lub a² = −128 odrzucam.

	1
Objętość V =		* 2a√3 * 6a * 5√5 = 20a2√15 = 60√3
	3

gratis: 60 √15

bonus: Oczywiście 60√15, chochlik, dla gratis