Oblicz pole powstałego przekroju.
HEJ: Potrzebuję pomocy....
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 12 i wysokości 8
poprowadzono przekrój przechodzący przez krawędź podstawy i środki przeciwległych
krawędzi bocznych. Oblicz pole powstałego przekroju.
16 mar 15:27
a7:
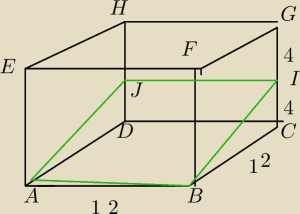
BI=
√144−16=8
√2
P=8
√2*12=96
√2
16 mar 15:37
Mila:
a7, miał być ostrosłup.
16 mar 15:41
a7: aaa, sorry
16 mar 15:42
HEJ: Ktoś coś?

16 mar 19:27
Eta:
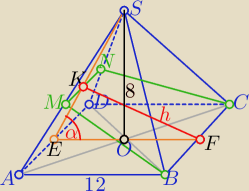
Przekrojem jest trapezBMNC o podstawach a=12 i b= 6 i wysokości h=|KF|
| | 3 | |
1/ wΔEOS cosα= |
| i |ES|=10 , |OE|=6 H=8 |
| | 4 | |
2/ z tw. cosinusów w ΔEFK
h
2=..............
i P
trapezu= ...........
i po ptokach

16 mar 20:13
Mila:
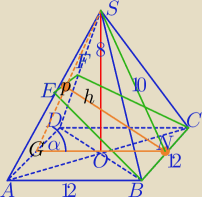
|EF|=6
1) W ΔSOG:
|GS|
2=6
2+8
2
|GS|=10
|PG|=5
2)
W ΔPGN:
h
2=5
2+12
2−2*5*12 cosα
h
2=169−72=97
h=
√97
================
h − II sposób
h obliczone bez trygonometrii:
W ΔSGN z tw. Apolloniusza:
h jest środkową
12
2+10
2=2*(h
2+25}
122=h
2+25
h
2=97
h=
√97
=====
16 mar 20:34
Mila:
O już jest!

, miałam przerwę na kolację w środku pisania.
16 mar 20:36
Eta:
Oczywiście miało być
16 mar 20:38
HEJ: Super, jesteście niesamowite!
16 mar 20:40
 BI=√144−16=8√2
P=8√2*12=96√2
BI=√144−16=8√2
P=8√2*12=96√2

 Przekrojem jest trapezBMNC o podstawach a=12 i b= 6 i wysokości h=|KF|
Przekrojem jest trapezBMNC o podstawach a=12 i b= 6 i wysokości h=|KF|

 |EF|=6
1) W ΔSOG:
|GS|2=62+82
|GS|=10
|PG|=5
|EF|=6
1) W ΔSOG:
|GS|2=62+82
|GS|=10
|PG|=5
 , miałam przerwę na kolację w środku pisania.
, miałam przerwę na kolację w środku pisania.