Oblicz obwód powstałego przekroju. mak: Sześcian o krawędzi 6 przecięto płaszczyzną przechodzącą przez przekątną jednej ze ścian i nachyloną do niej pod kątem 60 stopni. Oblicz obwód powstałego przekroju. Długości dwóch podstaw są mi znane, ale jak wyznaczyć ramiona?

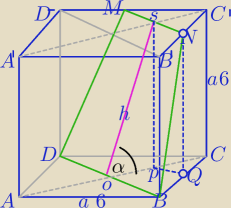
Mila: Przekrój jest Δrównoramiennym dla α∊(0,α₀), α₀≈54,7^o Przekrój jest trapezem równoramiennym dla kąta α∊(α₀,90) 1) |OC|=3√2

	h√3
|PS|=6, 6=
	2

h=4√3 |OP|=2√3 |PC|=3√2−2√3 2) ΔCPQ∼ΔCOB

CP		CO
	=
PQ		OB

3√2−2√3
	=1
PQ

|PQ|=3√2−2√3 3) |CQ|=(3√2−2√3)√2=6−2√3 |BN|²=6²+(2√3)²=36+12=48 |BN|=4√3=|DM| Obw.=6√2+2(3√2−2√3)+8√3=12√2+4√3

www: https://matematykaszkolna.pl/strona/692.html

Eta: Korzystam z rys. Mili 1/ z Δ OPS "ekierki" |OP|=2√3, h=|OS|=4√3 |PS|=6 2/ z podob. ΔOBC i ΔCPQ

	6√2		3√2
		=		⇒ b= 2(3√2−2√3)
	b		3√2−2√3

P_przekroju= (12√2−4√3)*2√3 P= 24(√6−1) ===========

chichi: a dlaczego liczymy pole przekroju jak pytają o obwód?

Jolanta: Bo panie od lat z tego słyną,że jak pomagają to bardzo dokładnie .Każdy może zerknąć i czegoś się douczyć 🙂

ite: @chichi bo to jest odpowiedź do wersji dla drugiej grupy !

chichi: może być i tak, to się nazywa kompleksowa pomoc

mak: W odpowiedzi figuruje 12√2 + 4√15 − 4√3. Suma podstaw wyniosła mnie 12√2 − 4√3. Skąd wziąć resztę? Z góry dziękuje za pomoc!

Eta: Poprawną odpowiedż taka jak podała Mila : 12√2+4√3

mak: Dobrze, zaufam

Mila: W punkcie (3) mam pomyłkę: mak, Myślałam, że wychwycisz ten lapsus rachunkowy. Zawsze trzeba sprawdzać rachunki. |CQ|=(3√2−2√3)*√2=6−2√6 dalej z poprawką: |BN|²=6²+(2√6)²=36+24=60=4*15 |BN|=2√15=|DM| |MN|=2*(3√2−2√3) obw=6√2+6√2−4√3+4√15 Obw=12√2−4√3+4√15 Jeżeli masz pytania to pisz.

Mila: chichi teraz to nigdy nie wiadomo, czy pomagać, czy nie. Pewną trafną uwagę już gdzieś na ten temat wpisałeś. Zobaczyłam, że "wisi" zadanko, to w przerwie filmu nabazgrałam rozwiązanie i włączyłam aktualizację. Dzisiaj zobaczyłam, że jest tam błąd.

mak: Dziś sama zrobiłam to zadanie i wyszła mi poprawna odpowiedź. Niestety jedynie śledząc zadanie sama nie zauważyłam błędu