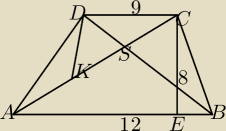
K jest środkiem odcinka AS i |AB|=12, |DC|=9, |CE|=h=8 ,
Oblicz pole trójkąta DKC
| 12 | 4 | 16 | ||||
PASB = x, ΔABS ∼ ΔDSC ⇒ k = | = | , zatem k2 = | ||||
| 9 | 3 | 9 |
| 9 | 4 | 9 | 192 | |||||
stąd PDSC = | x, PABCD = 84 = ( | + 1)2 | x ⇒ x = | , | ||||
| 16 | 3 | 16 | 7 |
| 4 | 9 | 192 | 144 | 72 | ||||||
PADS = | * | * | = | , PAKD = PSDK = | no to mamy: | |||||
| 3 | 16 | 7 | 7 | 7 |
| 72 | 108 | 180 | ||||
PDKC = | + | = | , masz odp. bo taki nieprzyjemny wynik?  | |||
| 7 | 7 | 7 |
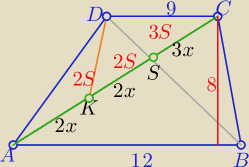Podobnie jak u chichi
| 4 | ||
skala podob. k= | to PDCS= 3S i PDKS=2S | |
| 3 |
| 7 | ||
P(trapezu)= 84 i P(trapezu)=(k+1)2*3S=84 ⇒ ( | )2 *S=28 | |
| 3 |
| 5*28*3*3 | 180 | |||
PDKC= 5S= | = | |||
| 7*7 | 7 |
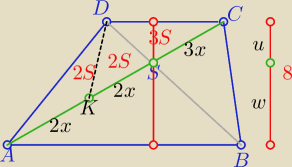Drugi sposób ........jak sugerował an
| 3 | 24 | |||
u= | *8= | |||
| 7 | 7 |
| 1 | 24 | |||
3S= | *9* | |||
| 2 | 7 |
| 5*3*12 | 180 | |||
to PDKC=5S= | = | |||
| 7 | 7 |