trapez Michał, proszę o pomoc!!: W trójkącie prostokątnym ABC dane są |AC|=12, |∠CAB|=60st. Poprowadzono prostą równoległą do przeciwprostokątnej AB dzielącą bok AC w stosunku 1:5, licząc od wierzchołka C. Prosta ta przecina bok AC w punkcie M, a bok BC w punkcie N. Oblicz pole trapezu ABNM.

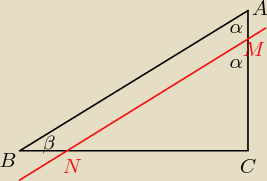
Basia: AC=12 α=60 ⇒ β=30

	AC
sinβ=
	AB

	12
sin30=
	AB

1		12
	=
2		AB

AB = 24

	BC
cosβ=
	AB

	BC
cos30=
	24

	√3
BC=24*
	2

BC=12√3

	AC*BC		12*12√3
PACB=		=		=72√3
	2		2

AM=x CM=5x AM+MC=AC 6x=12 x=2 MC=10 tr.ACB ~ tr.MCN

AC		MC
	=
BC		NC

12		10
	=
12√3		NC

1		10
	=
√3		NC

NC = 10√3

	MC*NC		10*10√3
PMCN=		=		= 50√3
	2		2

P_trapezu = P_ACB−P_MCN = 72√3−50√3=22√3

xyz: Wydaje mi się, że CM=x, a AM=5x i CN=y, BN=5y

Basia: a masz rację nie doczytałam , że "licząc od C"; wynik to zmienia, ale sposobu liczenia nie

smok: źle zrobione jest to zadanie.. odcinek AM=5x CM=x a nie odwrotnie