pierwiastek knaga: uzasadnij ze rownanie 3x⁵ − 10x³ + 20x −5 spelnia dokladnie jedna liczba rzeczywista z przedzialu <0; 1> czy wystarczy pokazac ze f(0) i f(1) maja rozne znaki i dlatego tam musi byc pierwiastek czy nie

getin: Jeszcze do tego trzeba wykazać monotoniczność w przedziale <0; 1>

knaga: dlaczego?

knaga: w sensie rozumiem ze trzeba wykazac z pochodnej ze w przedziale x ∊ R ma tylko jeden pierwiastek ale widze ze w rozwiazaniach licza jakies granice i nie wiem w jakim celu

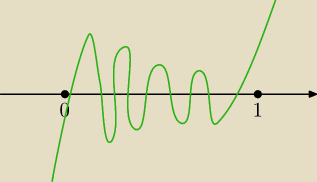
getin: Może być więcej rozwiązań tego równania jeśli nie pokażesz że funkcja jest rosnąca w przedziale <0; 1> lub malejąca w tym przedziale

knaga: no tak wykazalem ze pochodna jest zawsze dodatnia i skrocilem tak ze widac ze jest tylko jeden pierwiastek ale po co liczyc granice?

wredulus_pospolitus: ja nie widzę tutaj równania

knaga: hm

getin: Granic nie trzeba wg mnie bo to zwykły wielomian, wystarczy tylko aby pokazać że f(0)<0 oraz f(1)>0 oraz wykazać że pochodna jest zawsze dodatnia