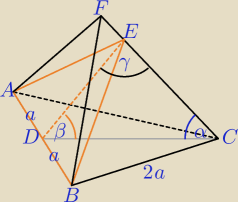
proszę o rozwiązanie anna: Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem α . Przez krawędź podstawy tego ostrosłupa poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod katem β , i która przecina przeciwległą krawędź ostrosłupa w punkcie E Oblicz stosunek pola powierzchni otrzymanego przekroju do pola powierzchni podstawy ostrosłupa jeżeli wiadomo, że 5sin α = 4sin(α + β ) .

Bogdan:

	sinα		4
5sinα = 4sin(α + β) ⇒		=
	sin(α + β)		5

sinγ = sin(α + β), |CD| = a√3,

	|DE|		|CD|
z twierdzenia sinusów w ΔDCE:		=		⇒ |DE| = ...
	sinα		sin(α + β)

Pola trójkątów: P_ABE = a*|DE| = ..., P_ABC = a*|CD| = ... Proszę kontynuować samodzielnie

anna: dziękuję