proszę o rozwiązanie anna: Rozpatrujemy wszystkie trójkąty równoramienne ABC (|AB | = |AC | ), na których opisano okrąg o promieniu R = 2 . Niech d oznacza długość ramienia AB trójkąta. Wykaż, że pole P każdego z tych trójkątów, jako funkcja długości d , wyraża się wzorem P(d) = ¹₁₆d³ √16 − d² . ja doszłam do wzoru P = ¹₂ IABI*ICDI ICDI = h = (2+x) I ABI =a P = ¹₂ * a * (2+x) z ΔADC IDCI² + IADI² = IACI² IACI = d − ramię ΔABC dalej nie mogę doprowadzić do wzoru P(d) = ¹₁₆d³ √16 − d² .

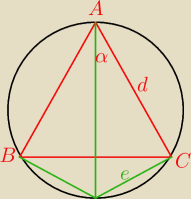
an: e=? sinα=? cosα=?

	d2sin2α		d3√16−d2
P=		=
	2		16

anna: dziękuję nie pomyślałam o dorysowaniu odpowiednich rysunków

wewe: Przypuszczam, że gdzieś się walnąłem licząc dziedzinę do tego zadania. Pole maksymalne wychodzi mi dla d=4 (też nie wiem czy dobrze), ale dziedzina mi wyszła (0,4), więc coś jest nie tak. Mógłby ktoś podesłać poprawne wyniki? I najlepiej jaka wyszła pochodna z funkcji