ostrosłup Miśka: Ostrosłup czworokątny prawidłowy o krawędzi podstawy długości α i wysokości długości a √2 przecięto płaszczyzną przechodzącą przez środki dwóch krawędzi bocznych ostrosłupa wychodzącychz przeciwległych wierzchołków podstawy i wierzchołek podstawy nie należący do żadnej z tych krawędzi. Jedna z płaszczyzn symetrii tego ostrosłupa dzieli otrzymany przekrój na dwa trójkąty o różnych polach. Oblicz obwód tego trójkąta, który ma większe pole.

Bogdan:

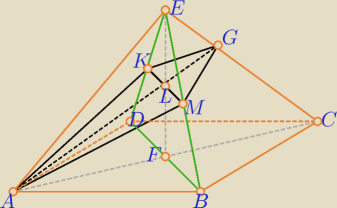
	√2
|AB| = |BC| = |CD| = |DA| = a, |FL| = |LE| =		,
	2

	a√2
|AF| = |FC| = |BF| = |FD| = |KM| =		(dlaczego?)
	2

|BM| = |ME| = |DK| = |KE| = ... Zachęcam do samodzielnego kontynuowania