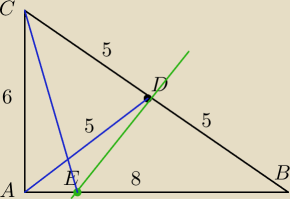
W trójkącie prostokątnym Elza: W trójkącie prostokątnym ABC przyprostokątne AB i AC mają odpowiednio długości: AB =8 i AC=6, punkt D jest środkiem przeciwprostokątnej BC. Prosta k jest prostopadła do BC, przechodzi przez punkt D i przecina bok AB w punkcie E. Uzasdadnij, że trójkąty ABD i BCE są podobne.

a7:

Elza: Skąd wiadomo, że AD ma 5?

Elza: Dziękuję bardzo za rysunek Nie wiem, co dalej ...

chichi:

	1
|AD| = R = 5 =		|CB|, jak nie znasz własności trójkąta prostokątnego to trudno
	2

rozwiązywać zadania, poszperaj i poszukaj własności nt. tego trójkąta

Elza: Dziękuję bardzo za pomoc, miałam zaćmienie, już rozwiązałam obydwa zadania. Pozdrawiam

a6: Ludzie w tym wieku Elzo nie maja zaćmienia, są po porostu niedouczeniu albo głupi

Mariusz: 2 mar 2023 21:44 Można to też pokazać z twierdzenia cosinusów x² = 6²+5²−2*5*6*cos(α)

	π
x2 = 82+52−2*5*8*cos(		− α)
	2

x² = 61 − 60cos(α) x² = 89 − 80sin(α) 0 = 28 + 60cos(α) − 80sin(α) 60cos(α) − 80sin(α) = −28

3		4		7
	cos(α) −		sin(α) = −
5		5		25

	3
cos(β) =
	5

	4
sin(β) =
	5

	7
cos(α+β) = −
	25

1		25
	= −
cos(α+β)		7

1		625
	=
cos2(α+β)		49

	625
1+tg2(α+β) =
	49

	576
tg2(α+β) =
	49

	24
tg(α+β) = −
	7

4   tg(α)+   3		24
	= −
4   1− tg(α)   3		7

3tg(α)+4		24
	= −
3−4tg(α)		7

7(3tg(α)+4) = −24(3−4tg(α)) 21tg(α) + 28 = −72 + 96tg(α) 75tg(α) = 100

	4
tg(α) =
	3

	1
1+tg2(α) =
	cos2(α)

	16		1
1+		=
	9		cos2(α)

25		1
	=
9		cos2(α)

9
	= cos2(α)
25

3		π
	= cos(α) , α ∊<0,		>
5		2

x² = 61 − 60cos(α)

	3
x2 = 61 − 60*
	5

x² = 61 − 36 x² = 25

turysta: A ten znów "pojechał" z Gdańska do Sopotu przez Rzym

Elza: Dziękuję za pomoc wszystkim życzliwym i zaangażowanym❤️. Jesteście wielcy. A6 nie chcę sobie wyobrażać, jak smutne musi być Twoje życie. Mam nadzieję, że ten komentarz ulżył trochę Twojej nienawiści do świata i ludzi . W przerwach między rozwiązywaniem zadań, podnieś głowę i spójrz czasem na drugiego człowieka. Może coś zobaczysz.

Mariusz: Elza drugi taki to ten turysta ale psy zawsze będą szczekać Co do długości odcinka AD to twierdzenie cosinusów jest nawet bardziej ogólne od tego co napisał chichi bo wystarczy znać długości boków trójkąta i stosunek w jakim punkt D dzieli długość boku BC i z twierdzenia cosinusów można łatwo obliczyć długość odcinka AD

Mariusz: Kontynuując wpis 3 mar 2023 08:23

	4
Z ΔABC wiemy że cos(β) =
	5

	5
Z ΔBDE wiemy że cos(β) =
	8−x

	4		5
Mamy zatem		=
	5		8−x

32 − 4x = 25 32 − 25 = 4x 4x = 7

	7
x =
	4

	7
|AE| =
	4

	25
|EB| =
	4

Z twierdzenia Pitagorasa w trójkącie CAE

	49
62+		=|CE|2
	16

	49
36+		=|CE|2
	16

36*16		49
	+		=|CE|2
16		16

576+49
	= |CE|2
16

625
	= |CE|2
16

	25
|CE| =
	4

Zatem trójkąt CEB jest równoramienny Teraz łatwo jest wykorzystać zarówno cechę kąt kąt kąt jak i cechę bok bok bok

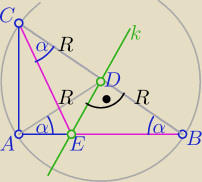
Eta: Prawie bez obliczeń k −− jest symetralną odcinka BC ⇒ |EB|=|EC| co oznacza ,że ΔBEC jest równoramienny o kątach |∡EBC|=|∡ECB|= α i ΔABD też równoramienny o kątach α przypodstawie zatem z cechy (kkk) ΔABD∼ΔBCE i po ptokach

chichi: ojj tam @Eta wymyślasz, przecież rozwiązanie @Mariusz jest tak proste, oczywiste i tak błyskawiczne, że nie opłaca się proponować innych rozwiązań

Mariusz: Rozwiązanie które przedstawiłem jest proste i oczywiste Rozwiązanie Ety całkiem niezłe i krótsze

Mariusz: https://link.springer.com/book/10.1007/978-1-4612-0963-8 chichi widziałeś tę książkę ? Pozycja starsza od ciebie ale może coś dla siebie znajdziesz