funkcje trygonometryczne Elza: Rozwiąż równanie: 4 ∥sinx∥ + 2 cos2x=3 w przedziale (0,3π). P.S. Błagam o pomoc − mam dwa zadanka, które mnie wykończą. Te kreski to wartość bezwzględna

chichi: 4|sin(x)| + 2cos(2x) = 3 4|sin(x)| + 2[1 − 2sin²(x)] = 3 teraz podstaw u = |sin(x)|, rozwiąż równanie kwadratowe i wróć do podstawienie. 4u + 2(1 − 2u²) = 3 P.S. u ∊ [0,1]

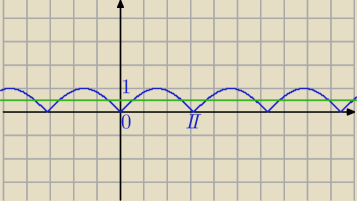
Mila: x∊(0,3π) 4|sin(x)|+2cos(2x)=3⇔ 4|sin(x)|+2*(1−2sin²(x))−3=0 4|sin(x)|−4sin²(x)−1=0 sin²(x)=(|sin(x)|² |sin(x)|=t, t∊<0,1> 4t²−4t+1=0 Δ=0

	1
t=
	2

	1
|sin(x)|=
	2

	π		5π
x=		+kπ lub x=		+kπ
	6		6

teraz podstawiaj za k kolejno {0,1,2,.., } aby wybrać rozwiązania z podanego przedziału.

Mila:

Elza: Dziękuję bardzo za pomoc i zaangażowanie❤️. Dobrze wiedzieć, że są jeszcze ludzie, którzy pomogą bezinteresownie, bez wyszydzania i wywyższania. Miłego wieczoru.