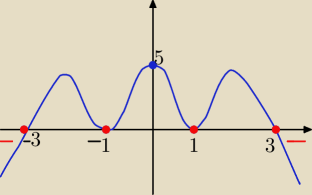
Wielomian P sommer: Znajdź wzór wielomianu P zmiennej x, spełniającego jednocześnie podane warunki: a) wielomian P jest wielomianem 6 stopnia, b) wielomian P jest funkcją parzystą, c) wykres przecina oś OY w punkcie o rzędnej 5, d) ma cztery miejsca zerowe, e) suma współczynników wynosi 0, f) przyjmuje wartości ujemne jedynie dla x∊(−∞;−3)∪(3;∞). Podaj uzasadnienie znaczenia poszczególnych warunków. nie wiem jak za to się zabrać

ite: Potraktuj to jako inspirację https://www.wolframalpha.com/input?i2d=true&i=-Divide%5B5%2C9%5D%5C%2840%29x%2B3%5C%2841%29%5C%2840%29x-3%5C%2841%29Power%5B%5C%2840%29x-1%5C%2841%29%2C2%5DPower%5B%5C%2840%29x%2B1%5C%2841%29%2C2%5D

sommer: to chyba za dużo dla mnie, jak do tego dojść?

Eta: b/ ⇒ wynika,że pierwiastki są symetryczne względem osi OY e) ⇒W(1)=0 to oznacza,że x=1 jest pierwiastkiem a więc z b) i x= −1 też jest pierwiastkiem f) ⇒ pierwiastkami są x= 3 i x= −3 oraz x= −1 i x= 1 −−− są pierwiastkami dwukrotnymi i współczynnik a <0 to W(x) = a(x²−9)((x−1)² (x+1)²

	5
z c) ⇒ W(0)= 5 to mamy : a*(−9)*1*1=5 ⇒ a= −
	9

	5
zatem W(x)= −		(x2−9)(x−1)2(x+1)2 ( st. 6
	9

=========================

Eta:

sommer: dzięki wielkie